题目内容
8.已知抛物线y=ax2+bx+c中,4a-b=0,a-b+c>0,抛物线与x轴有两个不同的交点,且这两个交点之间的距离小于2,则下列结论:①abc<0,②c>0,③a+b+c>0,④4a>c,其中结论正确的是( )
| A. | ①② | B. | ②③④ | C. | ①②③ | D. | ①②③④ |
分析 根据题意画出相应的图形,由图象可得出a,b及c都大于0,即可对选项①和②作出判断,由x=1时对应的函数值在x轴上方,故将x=1代入函数解析式,得到a+b+c大于0,可得出选项③正确,由抛物线与x轴有两个不同的交点,得到根的判别式大于0,然后将其中的b换为4a,整理后可得出4a大于c,得到选项④正确,综上,得到正确的选项有3个.
解答 解:∵抛物线y=ax2+bx+c中,4a-b=0,a-b+c>0,
∴抛物线对称轴为直线x=-$\frac{b}{2a}$=-$\frac{4a}{2a}$=-2,且x=-1对应二次函数图象上的点在x轴上方,
又这两个交点之间的距离小于2,根据题意画出相应的图形,如图所示: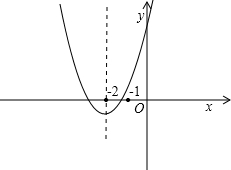
可得:a>0,b>0,c>0,
∴abc>0,故选项①错误,选项②正确;
由图象可得:当x=1时,y=a+b+c>0,故选项③正确;
∵抛物线与x轴有两个不同的交点,
∴b2-4ac>0,又4a-b=0,即b=4a,
∴(4a)2-4ac>0,即4a(4a-c)>0,
∴4a-c>0,即4a>c,故选项④正确,
综上,正确的选项有②③④共3个.
故选B
点评 此题考查了二次函数图象与系数的关系,利用了数形结合的思想,根据题意画出相应的图形是解本题的关键.

练习册系列答案
相关题目
16.关于函数y=-2x,下列叙述正确是( )
| A. | 函数图象经过点(1,2) | B. | 函数图象经过第三、四象限 | ||
| C. | y随x的增大而减小 | D. | 不论x取何值,总有y<0 |
13.有理数(-3)4与-34( )
| A. | 互为相反数 | B. | 互为倒数 | C. | 相等 | D. | 和为-28 |

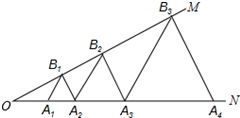 如图,已知:∠MON=30°,点A1、A2、A3 在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=a,则△A6B6A7的边长为32.
如图,已知:∠MON=30°,点A1、A2、A3 在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=a,则△A6B6A7的边长为32.