题目内容
3. 如图,在⊙O中,弦AB=1cm,圆周角∠ACB=30°,则⊙0的直径为2cm.
如图,在⊙O中,弦AB=1cm,圆周角∠ACB=30°,则⊙0的直径为2cm.
分析 由题意知,弦长为1所对的圆周角为30°,则弦对的圆心角为60°,由于弦与圆心构成的三角形是等腰三角形,所以当圆心角为60°,这个三角形是等边三角形,边长已知,易得半径,得直径.
解答 解:连接OA和OB,
∵AB=1,∠ACB=30°,
∴∠AOB=60°,
∵OA=OB,
∴三角形AOB为等边三角形,
∴OA=OB=AB=1,
∴直径为2cm,
故答案为:2.
点评 本题主要考查了圆周角定理和含有30度得直角三角形的知识点,利用(1)同一弦所对的圆周角是所对的圆心角的一半;(2)等边三角形的判定:有一角为60°的等腰三角形是等边三角形是解答此题的关键.

练习册系列答案
相关题目
14.下列说法中正确的是( )
| A. | 经过三点可以确定一个圆 | B. | 圆的切线垂直于半径 | ||
| C. | 对角线垂直的平行四边形是矩形 | D. | 对角线相等的菱形是正方形 |
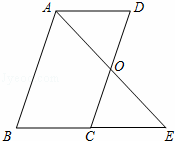 已知:如图,?ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
已知:如图,?ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E. 如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点. 如图,∠1=32°,∠2=75°,∠4=32°,则∠5=75°.
如图,∠1=32°,∠2=75°,∠4=32°,则∠5=75°. 如图,在△ABC中,∠B=∠C,D、E、F分别在AB、BC、AC上,且BD=CE,∠DEF=∠B,问:∠EDF与∠EFD是否相等?并说明理由.
如图,在△ABC中,∠B=∠C,D、E、F分别在AB、BC、AC上,且BD=CE,∠DEF=∠B,问:∠EDF与∠EFD是否相等?并说明理由.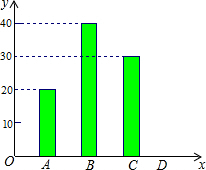 “五•一”假期,某公司组织部分员工分别到A、B、C、D四地旅游,公司按定额购买了前往各地的车票.如图是未制作完的车票种类和数量的条形统计图,根据统计图回答下列问题:
“五•一”假期,某公司组织部分员工分别到A、B、C、D四地旅游,公司按定额购买了前往各地的车票.如图是未制作完的车票种类和数量的条形统计图,根据统计图回答下列问题: 如图,矩形OABC的两边OA,OC在坐标轴上,且OC=2OA,M,N分别为OA,OC的中点,BM与AN交于点E,且四边形EMON的面积为2,
如图,矩形OABC的两边OA,OC在坐标轴上,且OC=2OA,M,N分别为OA,OC的中点,BM与AN交于点E,且四边形EMON的面积为2,