题目内容
5.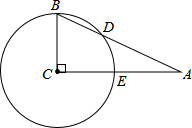 如图,在Rt△ABC中,∠C=90°,∠A=26°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则$\widehat{BD}$的度数为52°.
如图,在Rt△ABC中,∠C=90°,∠A=26°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则$\widehat{BD}$的度数为52°.
分析 连结CD,如图,先利用互余计算出∠B=64°,再利用半径相等和等腰三角形的性质得到∠CDB=∠B=64°,则根据三角形内角和定理可计算出∠BCD,然后根据圆心角的度数等于它所对弧的度数求解.
解答 解:连结CD,如图,
∵∠C=90°,∠A=26°,
∴∠B=64°,
∵CB=CD,
∴∠CDB=∠B=64°,
∴∠BCD=180°-64°-64°=52°,
∴$\widehat{BD}$的度数为52°.
故答案为52°.
点评 本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.

练习册系列答案
相关题目
20.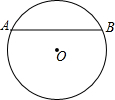 如图,在⊙O中,弦AB的长为24cm,圆心O到AB的距离为5cm,则⊙O的半径长为( )
如图,在⊙O中,弦AB的长为24cm,圆心O到AB的距离为5cm,则⊙O的半径长为( )
 如图,在⊙O中,弦AB的长为24cm,圆心O到AB的距离为5cm,则⊙O的半径长为( )
如图,在⊙O中,弦AB的长为24cm,圆心O到AB的距离为5cm,则⊙O的半径长为( )| A. | 24cm | B. | 13cm | C. | 14cm | D. | 15cm |
 如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB、BC于D、E,求$\frac{DE}{BC}$的值.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB、BC于D、E,求$\frac{DE}{BC}$的值. 如图,看图填空:
如图,看图填空: 如图,在△ABC中,AF:FD=1:5,BD=DC,求AE:EC的值.
如图,在△ABC中,AF:FD=1:5,BD=DC,求AE:EC的值.