题目内容
2.抛物线y=$\frac{1}{2}$(x+1)2+3的顶点坐标( )| A. | (1,3) | B. | (1,-3) | C. | (-1,-3) | D. | (-1,3) |
分析 抛物线y=a(x-h)2+k,顶点坐标是(h,k),直接根据抛物线y=2(x+1)2+3写出顶点坐标则可.
解答 解:顶点坐标是(-1,3).
故选D.
点评 本题考查由抛物线的顶点坐标式写出抛物线顶点的坐标,比较容易.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
12. 如图,已知点A(-1,0)和点B(1,2),在x轴上确定点P,使得△ABP为等腰三角形,则满足这样条件的点P共有( )
如图,已知点A(-1,0)和点B(1,2),在x轴上确定点P,使得△ABP为等腰三角形,则满足这样条件的点P共有( )
 如图,已知点A(-1,0)和点B(1,2),在x轴上确定点P,使得△ABP为等腰三角形,则满足这样条件的点P共有( )
如图,已知点A(-1,0)和点B(1,2),在x轴上确定点P,使得△ABP为等腰三角形,则满足这样条件的点P共有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
13.等腰三角形一边等于5,另一边等于8,则其周长是( )
| A. | 18 | B. | 21 | C. | 18或21 | D. | 不能确定 |
10.如果a2=9,那么a等于( )
| A. | 3 | B. | -3 | C. | 9 | D. | ±3 |
17.下列能组成三角形的线段是( )
| A. | 3cm、3cm、6cm | B. | 3cm、4cm、5cm | C. | 2cm、4cm、6cm | D. | 3cm、6cm、9cm |
7.已知⊙O的半径是5,OP的长为7,则点P与⊙O的位置关系是( )
| A. | 点P在圆内 | B. | 点P在圆上 | C. | 点P在圆外 | D. | 不能确定 |
14.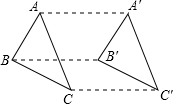 如图,△ABC沿着AA′方向平移到△A′B′C′,下列说法正确的是( )
如图,△ABC沿着AA′方向平移到△A′B′C′,下列说法正确的是( )
 如图,△ABC沿着AA′方向平移到△A′B′C′,下列说法正确的是( )
如图,△ABC沿着AA′方向平移到△A′B′C′,下列说法正确的是( )| A. | AB与A′B′平行但不相等 | B. | AB与A′B′相等但不平行 | ||
| C. | AB与A′B′平行且相等 | D. | 无法确定AB与A′B′的关系 |
12.-(+2)的相反数是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |