题目内容
3.(1)解方程组:$\left\{\begin{array}{l}{x-y=4①}\\{3x+y=16②}\end{array}\right.$(2)解不等式组:$\left\{\begin{array}{l}{2x+1<-1}\\{3-x≥1}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)求出不等式组中两不等式的解集,找出解集的公共部分即可.
解答 解:(1)①+②得:4x=20,即x=5,
把x=5代入①得:y=1,
则方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{2x+1<-1①}\\{3-x≥1②}\end{array}\right.$,
由①得:x<-1,
由②得:x≤2,
则不等式组的解集为x<-1.
点评 此题考查了解二元一次方程组,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
14.下列运算正确的是( )
| A. | a•a2=a2 | B. | a2+a2=a4 | C. | a6÷a2=a3 | D. | (2a)2=4a2 |
18.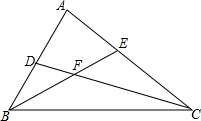 在△ABC中,如图,CD平分∠ACB,BE平分∠ABC,CD与BE交于点F,若∠DFE=120°,则∠A=( )
在△ABC中,如图,CD平分∠ACB,BE平分∠ABC,CD与BE交于点F,若∠DFE=120°,则∠A=( )
 在△ABC中,如图,CD平分∠ACB,BE平分∠ABC,CD与BE交于点F,若∠DFE=120°,则∠A=( )
在△ABC中,如图,CD平分∠ACB,BE平分∠ABC,CD与BE交于点F,若∠DFE=120°,则∠A=( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
8.从近日召开的全市旅游局长座谈会上了解到,滨州将要进一步做强做大旅游产业,努力实现新突破,2015年力争实现旅游收入110亿,打造都市旅游品牌.其中110亿用科学记数法表示为( )
| A. | 1.1×108 | B. | 110×108 | C. | 1.1×1010 | D. | 0.11×1011 |
12. 如图是一个正方体的表面展开图,如果相对面上所标的两个数互为相反数,那么图中x的值是( )
如图是一个正方体的表面展开图,如果相对面上所标的两个数互为相反数,那么图中x的值是( )
 如图是一个正方体的表面展开图,如果相对面上所标的两个数互为相反数,那么图中x的值是( )
如图是一个正方体的表面展开图,如果相对面上所标的两个数互为相反数,那么图中x的值是( )| A. | 8 | B. | 3 | C. | 2 | D. | -3 |
13.已知a>b,则下列不等式关系中正确的是( )
| A. | ac>bc | B. | ac2>bc2 | C. | a-1>b+1 | D. | a+1>b-1 |
 (尺规作图,不用写作法,保留作图痕迹)
(尺规作图,不用写作法,保留作图痕迹)