题目内容
如图，直线l与双曲线交于A、C两点，将直线l绕点O顺时针旋转a度角（0°＜a≤45°），与双曲线交于B、D两点，则四边形ABCD的形状一定是 ．
【答案】分析：由于直线l与双曲线都是关于原点的中心对称图形，根据对称性可得OA=OC，OB=OD，由此即可判定四边形ABCD一定是平行四边形．
解答：解：∵直线l与双曲线是关于原点的中心对称图形，
而AC，BD是四边形ABCD的对角线，
根据对称性可得：OA=OC，OB=OD，
∴四边形ABCD的对角线互相平分，
故四边形ABCD的形状一定是平行四边形．
故填空答案：平行四边形．
点评：此题综合考查了反比例函数，正比例函数等多个知识点，此题难度稍大，综合性比较强，注意对各个知识点的灵活应用．
解答：解：∵直线l与双曲线是关于原点的中心对称图形，
而AC，BD是四边形ABCD的对角线，
根据对称性可得：OA=OC，OB=OD，
∴四边形ABCD的对角线互相平分，
故四边形ABCD的形状一定是平行四边形．
故填空答案：平行四边形．
点评：此题综合考查了反比例函数，正比例函数等多个知识点，此题难度稍大，综合性比较强，注意对各个知识点的灵活应用．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
如图，直线AB与双曲线的一个交点为点C，CD⊥x轴与点D，OD=2OB=4OA=4． 求一次函数和反比例函数的解析式．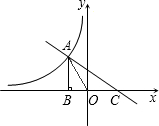
O|=4，点A的横坐标为-2，过点A作AB⊥x轴于点B，且S△AOC：S△AOB=3：2．
如图，直线l与双曲线交于A、B两点，C是线段BA延长线上的点，D是双曲线上一点（D都不与A、B重合），点C、D都在第一象限，过点C、D分别向x轴作垂线，垂足分别为E、F，连接OC、OD，设△COE的面积为S1，△DOF的面积为S2，则S1、S2的大小关系为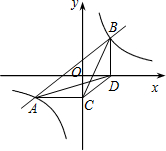
如图，直线AB与双曲线y=
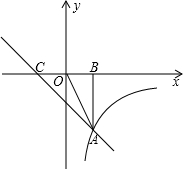轴于点B，且CO=2BO．