题目内容
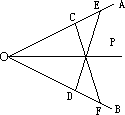
19、要画出∠AOB的平分线，分别在OA，OB上截取OC=OD，OE=OF，连接CF，DE，交于P点，那么∠AOB的平分线就是射线OP，要说明这个结论成立，可先说明△EOD≌△
FOC
，理由是SAS
，得到∠OED=∠OFC
，再说明△PEC≌△PFD
，理由是ASA
，得到PE=PF；最后说明△EOP≌△FOP
，理由是SSS
，从而说明了∠AOP=∠BOP，即OP平分∠AOB．分析：求∠AOB的平分线可利用三角形全等的性质作图．
解答：解：作法：
（1）分别在OA，OB上截取OC=OD，OE=OF，连接CF，DE，交于P点，
（2）连接OP即可，
∵OE=OF，∠EOF=∠EOF，OC=OD，
∴△EOD≌△FOC，∠OED=∠OFC，
在△PEC与△PFD中，∵∠OED=∠OFC，∠CPE=∠DPF，CE=DF，
∴△PEC≌△PFD，
故PE=PF，
在△EOP与△FOP中，OE=OF，PE=PF，OP=OP，
故△EOP≌△FOP，
故∠AOP=∠BOP，
即OP平分∠AOB．
（1）分别在OA，OB上截取OC=OD，OE=OF，连接CF，DE，交于P点，
（2）连接OP即可，
∵OE=OF，∠EOF=∠EOF，OC=OD，
∴△EOD≌△FOC，∠OED=∠OFC，
在△PEC与△PFD中，∵∠OED=∠OFC，∠CPE=∠DPF，CE=DF，
∴△PEC≌△PFD，
故PE=PF，
在△EOP与△FOP中，OE=OF，PE=PF，OP=OP，
故△EOP≌△FOP，
故∠AOP=∠BOP，
即OP平分∠AOB．
点评：此题考查了利用三角形全等求角平分线的方法，比较简便，是常用的方法．
练习册系列答案
相关题目
