题目内容
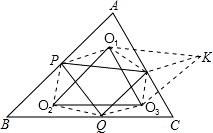 在△ABC的边AB,BC,CA上分别取点P,Q,S.证明以△APS,△BQP,△CSQ的外心为顶点的三角形与△ABC相似.
在△ABC的边AB,BC,CA上分别取点P,Q,S.证明以△APS,△BQP,△CSQ的外心为顶点的三角形与△ABC相似.
解:设O1,O2,O3是△APS,△BQP,
△CSQ的外心,作出六边形
O1PO2QO3S后再由外
心性质可知
∠PO1S=2∠A,
∠QO2P=2∠B,
∠SO3Q=2∠C.
∴∠PO1S+∠QO2P+∠SO3Q=360°.
从而又知∠O1PO2+∠O2QO3+∠O3SO1=360°
将△O2QO3绕着O3点旋转到△KSO3,易判断△KSO1≌△O2PO1,
同理可得△O1O2O3≌△O1KO3.
∴∠O2O1O3=∠KO1O3= ∠O2O1K
∠O2O1K
= (∠O2O1S+∠SO1K)
(∠O2O1S+∠SO1K)
= (∠O2O1S+∠PO1O2)
(∠O2O1S+∠PO1O2)
= ∠PO1S=∠A;
∠PO1S=∠A;
同理有∠O1O2O3=∠B.
故△O1O2O3∽△ABC.
分析:设O1,O2,O3是△APS,△BQP,△CSQ的外心,作出六边形,即可判定△KSO1≌△O2PO1,同时可得△O1O2O3≌△O1KO3,再求证∠O1O2O3=∠B即可得△O1O2O3∽△ABC.
点评:本题考查了相似三角形的证明,考查了相似三角形对应角相等的性质,考查了周角为360°的性质,考查了全等三角形的证明,考查了全等三角形对应角相等的性质,本题中求证∠O1O2O3=∠B是解题的关键.
△CSQ的外心,作出六边形
O1PO2QO3S后再由外
心性质可知
∠PO1S=2∠A,
∠QO2P=2∠B,
∠SO3Q=2∠C.
∴∠PO1S+∠QO2P+∠SO3Q=360°.
从而又知∠O1PO2+∠O2QO3+∠O3SO1=360°
将△O2QO3绕着O3点旋转到△KSO3,易判断△KSO1≌△O2PO1,
同理可得△O1O2O3≌△O1KO3.
∴∠O2O1O3=∠KO1O3=
 ∠O2O1K
∠O2O1K=
 (∠O2O1S+∠SO1K)
(∠O2O1S+∠SO1K)=
 (∠O2O1S+∠PO1O2)
(∠O2O1S+∠PO1O2)=
 ∠PO1S=∠A;
∠PO1S=∠A;同理有∠O1O2O3=∠B.
故△O1O2O3∽△ABC.
分析:设O1,O2,O3是△APS,△BQP,△CSQ的外心,作出六边形,即可判定△KSO1≌△O2PO1,同时可得△O1O2O3≌△O1KO3,再求证∠O1O2O3=∠B即可得△O1O2O3∽△ABC.
点评:本题考查了相似三角形的证明,考查了相似三角形对应角相等的性质,考查了周角为360°的性质,考查了全等三角形的证明,考查了全等三角形对应角相等的性质,本题中求证∠O1O2O3=∠B是解题的关键.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
如果点D、E分别在△ABC的边AB和AC上,那么下列比例式中能判定DE∥BC的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
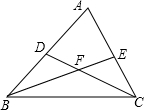 点D,E分别在△ABC的边AB,AC上,BE,CD相交于点F,设S四边形EADF=S1,S△BDF=S2,S△BCF=S3,S△CEF=S4,则S1S3与S2S4的大小关系为( )
点D,E分别在△ABC的边AB,AC上,BE,CD相交于点F,设S四边形EADF=S1,S△BDF=S2,S△BCF=S3,S△CEF=S4,则S1S3与S2S4的大小关系为( )| A、S1S3<S2S4 | B、S1S3=S2S4 | C、S1S3>S2S4 | D、不能确定 |
 如图,D、E分别在△ABC的边AB、AC上,且AD=
如图,D、E分别在△ABC的边AB、AC上,且AD= 22、如图,点D在△ABC的边AB上,连接CD,若要使△ABC∽△ACD,那么还需要添加的一个条件是
22、如图,点D在△ABC的边AB上,连接CD,若要使△ABC∽△ACD,那么还需要添加的一个条件是