题目内容
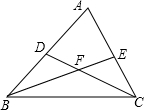点D，E分别在△ABC的边AB，AC上，BE，CD相交于点F，设S四边形EADF=S1，S△BDF=S2，S△BCF=S3，S△CEF=S4，则S1S3与S2S4的大小关系为（ ）| A、S1S3＜S2S4 | B、S1S3=S2S4 | C、S1S3＞S2S4 | D、不能确定 |
分析：首先作辅助线：连接DE，再设S△DEF=S′1，根据等高三角形的面积比等于对应底的比，可得：则
=
=
，则可证得：S1′S3=S2S4，即可得到：S1S3＞S2S4．
| S′1 |
| S2 |
| EF |
| BF |
| S4 |
| S3 |
解答：
解：如图，连接DE，设S△DEF=S′1，
则
=
=
，从而有S1′S3=S2S4．
因为S1＞S1′，所以S1S3＞S2S4．
故选C．
解：如图，连接DE，设S△DEF=S′1，则
| S′1 |
| S2 |
| EF |
| BF |
| S4 |
| S3 |
因为S1＞S1′，所以S1S3＞S2S4．
故选C．
点评：此题考查了有关三角形面积的求解．注意等高三角形的面积比等于对应底的比性质的应用．
练习册系列答案
相关题目
在△ABC中，∠A=90°，AB=8，BC=10，点M、N分别在AB、AC上．
（2013•河北）如图，四边形ABCD中，点M，N分别在AB，BC上，将△BMN沿MN翻折，得△FMN，若MF∥AD，FN∥DC，则∠B=
如图所示，△ABC中，点D、E分别在AB、BC边上，DE∥AC，∠B=50°，∠C=70°，那么∠1的度数为