题目内容
4.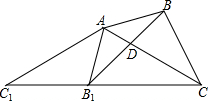 如图,△ABC中,∠BAC=45°,∠ACB=30°,将△ABC绕点A顺时针旋转得到△AB1C1,当点C1、B1、C三点共线时,旋转角为α,连接BB1,交AC于点D.下列结论:①△AC1C为等腰三角形;②△AB1D∽△BCD;③α=75°;④CA=CB1,其中正确的是( )
如图,△ABC中,∠BAC=45°,∠ACB=30°,将△ABC绕点A顺时针旋转得到△AB1C1,当点C1、B1、C三点共线时,旋转角为α,连接BB1,交AC于点D.下列结论:①△AC1C为等腰三角形;②△AB1D∽△BCD;③α=75°;④CA=CB1,其中正确的是( )| A. | ①③④ | B. | ①②④ | C. | ②③④ | D. | ①②③④ |
分析 将△ABC绕点A顺时针旋转得到△AB1C1,得到△ABC≌△AB1C1,根据全等三角形的性质得到AC1=AC,于是得到△AC1C为等腰三角形;故①正确;根据等腰三角形的性质得到∠C1=∠ACC1=30°,由三角形的内角和得到∠C1AC=120°,得到∠B1AB=120°,根据等腰三角形的性质得到∠AB1B=30°=∠ACB,于是得到△AB1D∽△BCD;故②正确;由旋转角α=120°,故③错误;根据旋转的性质得到∠C1AB1=∠BAC=45°,推出∠B1AC=∠AB1C,于是得到CA=CB1;故④正确.
解答 解:∵将△ABC绕点A顺时针旋转得到△AB1C1,
∴△ABC≌△AB1C1,
∴AC1=AC,
∴△AC1C为等腰三角形;故①正确;
∴AC1=AC,
∴∠C1=∠ACC1=30°,
∴∠C1AC=120°,
∴∠B1AB=120°,
∵AB1=AB,
∴∠AB1B=30°=∠ACB,
∵∠ADB1=∠BDC,
∴△AB1D∽△BCD;故②正确;
∵旋转角为α,
∴α=120°,故③错误;
∵∠C1AB1=∠BAC=45°,
∴∠B1AC=75°,
∵∠AB1C1=∠BAC=105°,
∴∠AB1C=75°,
∴∠B1AC=∠AB1C,
∴CA=CB1;故④正确.
故选B.
点评 本题考查了相似三角形的判定和性质,等腰三角形的判定和性质,旋转的性质,正确的识别图形是解题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
14.下列实数是无理数的是( )
| A. | -1 | B. | $\sqrt{3}$ | C. | 3.14 | D. | $\frac{1}{3}$ |
12.下列运算中.正确的是( )
| A. | x10÷(x4÷x2)=x8 | B. | (xy)5÷(xy)3=xy2 | ||
| C. | 2xn+2÷xn+1=x2 | D. | (6x3-3x2+3x)÷(3x)=2x2-x |
19.下列说法中,是真命题的是( )
| A. | 相等的角是对顶角 | |
| B. | 两条直线被第三条直线所截,内错角相等 | |
| C. | 若两条直线都和第三条直线平行,则这两条直线平行 | |
| D. | 若两个角的和为180°,则这两个角互为邻补角 |
 如图,在梯形ABCD中,AD∥BC,E是AB上一点,EF∥BC交CD于点F,AE:EB=1:2,AD=10,BC=25,求EF的长.
如图,在梯形ABCD中,AD∥BC,E是AB上一点,EF∥BC交CD于点F,AE:EB=1:2,AD=10,BC=25,求EF的长.