题目内容
 如图,△ABC中,∠C=90°,AD平分∠CAB,BC=4cm,AC=3cm,那么点D到AB的距离是
如图,△ABC中,∠C=90°,AD平分∠CAB,BC=4cm,AC=3cm,那么点D到AB的距离是考点:角平分线的性质
专题:
分析:过点D作DE⊥AB于E,根据角平分线上的点到角的两边的距离相等可得DE=CD,再利用“HL”证明Rt△ACD和Rt△AED全等,根据全等三角形对应边相等可得AC=AE,再根据勾股定理列式求出AB的长,设DE=x,表示出BD、BE的长,然后根据勾股定理列式进行计算即可得解.
解答: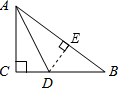 解:如图,过点D作DE⊥AB于E,
解:如图,过点D作DE⊥AB于E,
∵AD平分∠CAB,
∴DE=CD.
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
∵BC=4cm,AC=3cm,
∴AB=
=5cm,
设DE=x,则BD=BC-CD=4-x,
BE=AB-AE=5-3=2,
在Rt△BDE中,BD2=DE2+BE2,
∴(4-x)2=x2+22,
解得x=
,
即点D到AB的距离是
cm.
故答案为:
.
 解:如图,过点D作DE⊥AB于E,
解:如图,过点D作DE⊥AB于E,∵AD平分∠CAB,
∴DE=CD.
在Rt△ACD和Rt△AED中,
|
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
∵BC=4cm,AC=3cm,
∴AB=
| BC2+AC2 |
设DE=x,则BD=BC-CD=4-x,
BE=AB-AE=5-3=2,
在Rt△BDE中,BD2=DE2+BE2,
∴(4-x)2=x2+22,
解得x=
| 3 |
| 2 |
即点D到AB的距离是
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题考查了角平分线上的点到角的两边的距离相等的性质,勾股定理的应用,作辅助线构造出全等三角形与直角三角形是解题的关键.

练习册系列答案
相关题目
下列说法中正确的是( )
| A、无限小数都是无理数 |
| B、数轴上的点都表示有理数 |
| C、平方根等于它本身的是1和0 |
| D、立方根等于它本身的是-1、0和1 |
如图,①图由1张小正方形纸片组成,由6张同样大小的小正方形纸片可以组成②图,由15张同样大小的小正方形纸片可以组成③图,…,以此规律组成第⑤图需要的同样大小的小正方形纸片张数为( )


| A、28 | B、36 | C、45 | D、66 |
下列图案由边长相等的黑、白两色正方形按一定的规律拼接而成,依此规律,第n个图形中白色正方形的个数为( )


| A、4n+1 | B、4n-1 |
| C、3n-2 | D、3n+2 |
下列命题错误的是( )
| A、经过三个点一定可以作圆 |
| B、三角形的外心到三角形各顶点的距离相等 |
| C、同圆或等圆中,相等的圆心角所对的弧相等 |
| D、平分弦(不是直径)的直径垂直于弦 |
 已知在△ABC中,AD=BD,CE=EF=BF,S△AHD=10,求S四边形EFHG.
已知在△ABC中,AD=BD,CE=EF=BF,S△AHD=10,求S四边形EFHG.