题目内容
9. 问题探究:
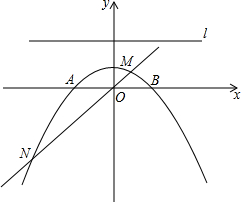
问题探究:抛物线y=-$\frac{1}{8}$x2+bx+2(b>0)与x轴交于A、B两点,交y轴于C,直线y=kx与抛物线交于M、N两点(M在y轴右边,k>0),点C(0,2),点AO=2CO
(1)求此抛物线的解析式
(2)若△AMN的面积为16$\sqrt{2}$时,求k的值
(3)己知直线l:y=t(t>2),是否存在这样的t的值,无论k取何值,以MN为直径的圆总与直线l相切?若存在,求t的值;若不存在,说明理由.
分析 (1)由条件可求得A点坐标,代入可求得b的值,可求得抛物线解析式;
(2)连接AM、AN,可设出M、N的坐标,利用三角形的面积和一元二次方程根与系数的关系可得大到关于k的方程,可求得k的值;
(3)同(2)设出M、N的坐标,分别表示出MO和NO的长,利用相切可得到t的方程,可求得t的值.
解答 解:
(1)∵y=-$\frac{1}{8}$x2+bx+2,
∴C(0,2),
∴AO=2OC=2×2=4,
∴A(-4,0),
代入抛物线解析式可得0=-2-4b+2,解得b=0,
∴抛物线解析式为y=-$\frac{1}{8}$x2+2;
(2)如图,连AM、AN,
设M(x1,y1),N(x2,y2),
∵M、N在直线y=kx上,
∴y1=kx1,y2=kx2,
∴S△AMN=S△AOM+S△AON=$\frac{1}{2}$AO•|y1|+$\frac{1}{2}$AO•|y2|=$\frac{1}{2}$AO•(y1-y2)=2k(x1-x2),
联立直线与抛物线解析式可得$\left\{\begin{array}{l}{y=kx}\\{y=-\frac{1}{8}{x}^{2}+2}\end{array}\right.$,整理可得:x2+8kx-16=0,
∵M、N在抛物线上,
∴x1,x2是方程的两根,
∴x1+x2=-8k,x1•x2=-16
∴x1-x2=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=8$\sqrt{{k}^{2}+1}$,
∴16k$\sqrt{{k}^{2}+1}$=16$\sqrt{2}$,解得k=1或k=-1(舍去),
∴k的值为1;
(3)设M(x1,y1),N(x2,y2),
则MO=$\sqrt{{x}_{1}^{2}+{y}_{1}^{2}}$=$\sqrt{(-\frac{1}{8}{x}_{1}^{2}+2)^{2}+{x}_{1}^{2}}$=$\sqrt{(-\frac{1}{8}{x}_{1}^{2}-2)^{2}}$=$\frac{1}{8}$${x}_{1}^{2}$+2=4-y1,
同理NO=4-y2,
∴MN=8-(y1+y2),即r=4-$\frac{{y}_{1}+{y}_{2}}{2}$,
设圆心为G,则yG=$\frac{{y}_{1}+{y}_{2}}{2}$,
∴G到l的离d=t-$\frac{{y}_{1}+{y}_{2}}{2}$,
要使直线l与⊙G相切,则d=r,
∴t=4,
即存在满足条件的t,其值为4.
点评 本题为二次函数的综合应用,涉及待定系数法、函数图象的交点、一元二次方程根与系数的关系、勾股定理、直线和圆相切的判定和性质及方程思想等知识点.在(1)中求得A点坐标是解题的关键,在(2)中用M、N的坐标表示出△AMN的面积是解题的关键,在(3)中用M、N的坐标分别表示出圆心坐标是解题的关键.本题考查知识点较多,综合性较强,计算量较大,故难度较大.

 如图,数轴上有A,B,C,D四个点,其中所对应的数的绝对值最大的点是( )
如图,数轴上有A,B,C,D四个点,其中所对应的数的绝对值最大的点是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
| A. | 当d=8 cm时,点P在⊙O外 | B. | 当d=10 cm时,点P在⊙O上 | ||
| C. | 当d=5 cm时,点P在⊙O内 | D. | 当d=0 cm时,点P在⊙O上 |
| A. | 5a-3a=2 | B. | -2x2y+3xy2=x2y | ||
| C. | 4x2-3x=x | D. | -6a2b-6a2b=-12a2b |
 如图,在△ABC中,AB=6cm,BC=12cm,动点P从A开始沿AB边运动,速度为2cm/s;动点Q从点B开始沿BC边运动,速度为4cm/s;t=$\frac{3}{2}$s或$\frac{3}{5}$s,由P、B、Q三点连成的三角形与△ABC相似.
如图,在△ABC中,AB=6cm,BC=12cm,动点P从A开始沿AB边运动,速度为2cm/s;动点Q从点B开始沿BC边运动,速度为4cm/s;t=$\frac{3}{2}$s或$\frac{3}{5}$s,由P、B、Q三点连成的三角形与△ABC相似.