Question

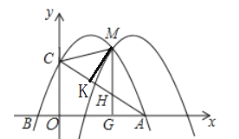
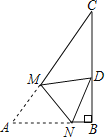
【题目】如图，已知Rt△ABC中，∠B＝90°，∠A＝60°，AB＝3，点M，N分别在线段AC，AB上，将△ANM沿直线MN折叠，使点A的对应点D恰好落在线段BC上，若△DCM为直角三角形时，则AM的长为_____．

Answer 1

【答案】2或3﹣3

【解析】

依据△DCM为直角三角形，需要分两种情况进行讨论：当∠CDM＝90°时，△CDM是直角三角形；当∠CMD＝90°时，△CDM是直角三角形，分别依据含30°角的直角三角形的性质以及等腰直角三角形的性质，即可得到AM的长．

解：分两种情况：

①如图，当∠CDM＝90°时，△CDM是直角三角形，

∵在Rt△ABC中，∠B＝90°，∠A＝60°，AB＝3，

∴AC＝2AB＝6，∠C＝30°，由折叠可得，∠MDN＝∠A＝60°，

∴∠BDN＝30°，

∴BN＝DN＝AN，

∴BN＝AB＝1，

∴AN＝2BN＝2，

∵∠DNB＝60°，

∴∠ANM＝∠DNM＝60°，

∴∠AMN＝60°，

∴AM＝AN＝2；

②如图，当∠CMD＝90°时，△CDM是直角三角形，

由题可得，∠CDM＝60°，∠A＝∠MDN＝60°，

∴∠BDN＝60°，∠BND＝30°，

∴BD＝DN＝AN，BN＝BD，

又∵AB＝3，

∴AN＝6（2﹣），BN＝6﹣9，

过N作NH⊥AM于H，则∠ANH＝30°，

∴AH＝AN＝3（2﹣），HN＝6﹣9，

由折叠可得，∠AMN＝∠DMN＝45°，

∴△MNH是等腰直角三角形，

∴HM＝HN＝6﹣9，

∴AM＝AH+HM＝3（2﹣）+6﹣9＝3﹣3，

故答案为：2或3﹣3．