题目内容
 如图.⊙O中,AB是直径,AD是弦,过B点的切线与AD的延长线交于点C,若AD=CD,则tan∠OCA值是
如图.⊙O中,AB是直径,AD是弦,过B点的切线与AD的延长线交于点C,若AD=CD,则tan∠OCA值是
- A.

- B.

- C.

- D.

A
分析:连接BD,过O作OM⊥AC于M,求出AM=OM,设OM=AM=a,则AO= =
= a,求出AB=BC=2ao=2
a,求出AB=BC=2ao=2 a,由勾股定理求出AC=4a,求出CM=3a,代入tan∠OCA=
a,由勾股定理求出AC=4a,求出CM=3a,代入tan∠OCA= 求出即可.
求出即可.
解答: 解:连接BD,过O作OM⊥AC于M,
解:连接BD,过O作OM⊥AC于M,
∵AB是⊙O直径,
∴∠ADB=90°,
∴BD⊥AC,
∵AD=CD,
∴AB=BC,
∵BC切⊙O于B,
∴∠ABC=90°,
∴∠A=∠ACB=45°,
∵OM⊥AC,
∴∠AMO=90°,
∴∠AOM=45°=∠A,
∴AM=OM,
设OM=AM=a,则AO= =
= a,
a,
∴AB=BC=2ao=2 a,
a,
由勾股定理得:AC= =4a,
=4a,
∴CM=4a-a=3a,
∴tan∠OCA= =
=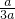 =
= ,
,
故选A.
点评:本题考查了等腰三角形性质和判定,切线的性质,勾股定理,解直角三角形的应用,主要考查学生的推理能力和计算能力.
分析:连接BD,过O作OM⊥AC于M,求出AM=OM,设OM=AM=a,则AO=
 =
= a,求出AB=BC=2ao=2
a,求出AB=BC=2ao=2 a,由勾股定理求出AC=4a,求出CM=3a,代入tan∠OCA=
a,由勾股定理求出AC=4a,求出CM=3a,代入tan∠OCA= 求出即可.
求出即可.解答:
 解:连接BD,过O作OM⊥AC于M,
解:连接BD,过O作OM⊥AC于M,∵AB是⊙O直径,
∴∠ADB=90°,
∴BD⊥AC,
∵AD=CD,
∴AB=BC,
∵BC切⊙O于B,
∴∠ABC=90°,
∴∠A=∠ACB=45°,
∵OM⊥AC,
∴∠AMO=90°,
∴∠AOM=45°=∠A,
∴AM=OM,
设OM=AM=a,则AO=
 =
= a,
a,∴AB=BC=2ao=2
 a,
a,由勾股定理得:AC=
 =4a,
=4a,∴CM=4a-a=3a,
∴tan∠OCA=
 =
=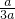 =
= ,
,故选A.
点评:本题考查了等腰三角形性质和判定,切线的性质,勾股定理,解直角三角形的应用,主要考查学生的推理能力和计算能力.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 如图,⊙O中,AB是直径,BC是⊙O的切线,AC交⊙O于点E,OD⊥AC于点D.已知⊙O的半径是2,BC=3,则CE=
如图,⊙O中,AB是直径,BC是⊙O的切线,AC交⊙O于点E,OD⊥AC于点D.已知⊙O的半径是2,BC=3,则CE= 如图,⊙O中,AB是直径,半径CO⊥AB,D是CO的中点,DE∥AB,求证:
如图,⊙O中,AB是直径,半径CO⊥AB,D是CO的中点,DE∥AB,求证:


 中,AB是⊙O的直径,
中,AB是⊙O的直径, ,
, ,
, 的度数是( )
的度数是( ) B.100
B.100
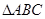 中,AB是⊙O的直径,
中,AB是⊙O的直径,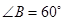 ,
,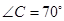 ,则
,则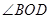 的度数是( )
的度数是( )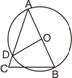
 B.100
B.100