题目内容
 如图,⊙O中,AB是直径,半径CO⊥AB,D是CO的中点,DE∥AB,求证:
如图,⊙O中,AB是直径,半径CO⊥AB,D是CO的中点,DE∥AB,求证: |
| EC |
 |
| EA |
分析:连接OE,推出DE⊥OC,求出∠EDO=90°,根据OD=
OC=
OE,求出∠DEO=30°,求出∠EOC,根据OC⊥AB,求出∠AOC=90°,求出∠AOE=30°,即可求出答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:
连接OE,
∵AB⊥OC,DE∥AB,
∴DE⊥OC,
∴∠EDO=90°,
∵D为OC中点,
∴OD=
OC=
OE,
∴∠DEO=30°,
∴∠EOC=90°-30°=60°,
∵OC⊥AB,
∴∠AOC=90°,
∴∠AOE=90°-60°=30°,
即∠AOE=30°,∠COE=60°,
∴
=2
(圆心角的度数等于它所对的弧的度数).

连接OE,
∵AB⊥OC,DE∥AB,
∴DE⊥OC,
∴∠EDO=90°,
∵D为OC中点,
∴OD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DEO=30°,
∴∠EOC=90°-30°=60°,
∵OC⊥AB,
∴∠AOC=90°,
∴∠AOE=90°-60°=30°,
即∠AOE=30°,∠COE=60°,
∴
 |
| EC |
 |
| EA |
点评:本题考查了三角形的内角和定理,平行线的性质和判定,圆心角、弧、弦之间的关系,和30度角的直角三角形,主要考查学生运用定理进行推理的能力,题目比较好,综合性比较强.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 如图,⊙O中,AB是直径,BC是⊙O的切线,AC交⊙O于点E,OD⊥AC于点D.已知⊙O的半径是2,BC=3,则CE=
如图,⊙O中,AB是直径,BC是⊙O的切线,AC交⊙O于点E,OD⊥AC于点D.已知⊙O的半径是2,BC=3,则CE=

 中,AB是⊙O的直径,
中,AB是⊙O的直径, ,
, ,
, 的度数是( )
的度数是( ) B.100
B.100
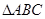 中,AB是⊙O的直径,
中,AB是⊙O的直径,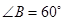 ,
,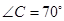 ,则
,则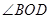 的度数是( )
的度数是( )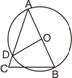
 B.100
B.100