题目内容
 如图,⊙O中,AB是直径,BC是⊙O的切线,AC交⊙O于点E,OD⊥AC于点D.已知⊙O的半径是2,BC=3,则CE=
如图,⊙O中,AB是直径,BC是⊙O的切线,AC交⊙O于点E,OD⊥AC于点D.已知⊙O的半径是2,BC=3,则CE=| 9 |
| 5 |
| 9 |
| 5 |
分析:如图,连接BE构建相似三角形△ABC∽△BEC,由相似三角形的对应边成比例得到
=
,而BE可由面积法求得其长度,从而得到CE的长.
| AB |
| BC |
| BE |
| EC |
解答: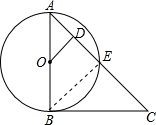 解:∵AB是直径,BC是⊙O的切线,
解:∵AB是直径,BC是⊙O的切线,
∴∠ABC=90°.
∴AC=
=5.
如图,连接BE.
∵AB是直径,
∴∠AEB=90°,
∴
AC•BE=
AB•BC,则BE=
=
.
∵∠ABC=∠BEC=90°,∠A=∠CBE(同角的余角相等),
∴△ABC∽△BCE,
∴
=
,
∴CE=
=
=
.
故答案是:
.
 解:∵AB是直径,BC是⊙O的切线,
解:∵AB是直径,BC是⊙O的切线,∴∠ABC=90°.
∴AC=
| AB2+BC2 |
如图,连接BE.
∵AB是直径,
∴∠AEB=90°,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| AB•BC |
| AC |
| 12 |
| 5 |
∵∠ABC=∠BEC=90°,∠A=∠CBE(同角的余角相等),
∴△ABC∽△BCE,
∴
| AB |
| BC |
| BE |
| EC |
∴CE=
| BC•BE |
| AB |
3×
| ||
| 4 |
| 9 |
| 5 |
故答案是:
| 9 |
| 5 |
点评:本题考查了切线的性质.运用切线的性质来进行计算或论证,常通过作辅助线,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,⊙O中,AB是直径,半径CO⊥AB,D是CO的中点,DE∥AB,求证:
如图,⊙O中,AB是直径,半径CO⊥AB,D是CO的中点,DE∥AB,求证:


 中,AB是⊙O的直径,
中,AB是⊙O的直径, ,
, ,
, 的度数是( )
的度数是( ) B.100
B.100
 中,AB是⊙O的直径,
中,AB是⊙O的直径,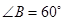 ,
,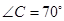 ,则
,则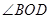 的度数是( )
的度数是( )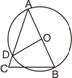
 B.100
B.100