Question

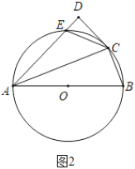
【题目】如图，在扇形中，，半径交弦于点，且，若，则阴影部分的面积为________．

Answer 1

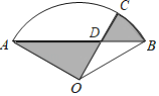
【答案】

【解析】

先计算出∠A=∠OBA=∠BOD=30°，则DO=DB，利用含30度的直角三角形三边的关系得到OD=，OD=，所以BD=，计算出S△AOD=得到S△BOD=S△AOD=，然后根据扇形的面积公式，利用阴影部分的面积=S△AOD+S扇形BOC-S△BOD进行计算．

解：∵∠AOB=120°，OA=OB，

∴∠A=∠OBA=30°，

∵OC⊥AO，

∴∠AOD=90°，

∴∠BOD=30°，

∴DO=DB，

在Rt△AOD中，OD=，OD=AD，

∴BD=AD，

∵S△AOD=×6×=，

∴S△BOD=S△AOD=

∴阴影部分的面积=S△AOD+S扇形BOC-S△BOD

=

故答案为．