题目内容
对于正数x,规定f(x)= ,比如 f(3)=
,比如 f(3)=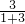 ,f
,f =
= ,则计算f(1)+f(2)+f(3)+…+f(99)+f(100)+f
,则计算f(1)+f(2)+f(3)+…+f(99)+f(100)+f +f
+f +…+f
+…+f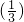 +f
+f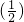 +f(1)=______.
+f(1)=______.
解:由题意得,f(1)= ,故f(1)+f(1)=1;
,故f(1)+f(1)=1;
f(2)= ,f(
,f( )=
)= ,故f(2)+f(
,故f(2)+f( )=1;
)=1;
f(3)= ,f(
,f( )=
)= ,故f(3)+f(
,故f(3)+f( )=1;
)=1;
…
故可得f(n)+f( )=1,
)=1,
故f(1)+f(2)+f(3)+…+f(99)+f(100)+f +f
+f +…+f
+…+f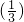 +f
+f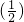 +f(1)=100.
+f(1)=100.
故答案为:100.
分析:仔细观察所给式子,然后根据f(1)+f(1)=1,f(2)+f( )=1,f(3)+f(
)=1,f(3)+f( )=1,…即可得出规律,继而可得出结果.
)=1,…即可得出规律,继而可得出结果.
点评:本题考查了分式的求值,解答此题的关键是理解好f(x)= ,同时对整理好的分式要注意观察特点,能够看出
,同时对整理好的分式要注意观察特点,能够看出 +
+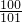 ,其他分式亦如此.
,其他分式亦如此.
 ,故f(1)+f(1)=1;
,故f(1)+f(1)=1;f(2)=
 ,f(
,f( )=
)= ,故f(2)+f(
,故f(2)+f( )=1;
)=1;f(3)=
 ,f(
,f( )=
)= ,故f(3)+f(
,故f(3)+f( )=1;
)=1;…
故可得f(n)+f(
 )=1,
)=1,故f(1)+f(2)+f(3)+…+f(99)+f(100)+f
 +f
+f +…+f
+…+f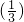 +f
+f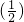 +f(1)=100.
+f(1)=100.故答案为:100.
分析:仔细观察所给式子,然后根据f(1)+f(1)=1,f(2)+f(
 )=1,f(3)+f(
)=1,f(3)+f( )=1,…即可得出规律,继而可得出结果.
)=1,…即可得出规律,继而可得出结果.点评:本题考查了分式的求值,解答此题的关键是理解好f(x)=
 ,同时对整理好的分式要注意观察特点,能够看出
,同时对整理好的分式要注意观察特点,能够看出 +
+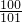 ,其他分式亦如此.
,其他分式亦如此. 
练习册系列答案
相关题目
 (1)对于正数x,规定f(x)=
(1)对于正数x,规定f(x)=