Question

【题目】在学习苏科版九下《锐角三角函数》一章时，小明同学对一个角的倍角的三角函数值是否具有关系产生了浓厚的兴趣，进行了一些研究．

（1）初步尝试：我们知道：tan60°＝　 　，tan30°＝　 　，发现结论：tanA　 　2tan∠A（填“＝”或“≠”）；

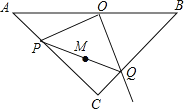
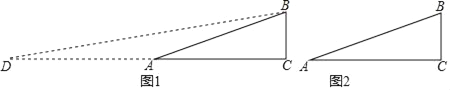
（2）实践探究：如图1，在Rt△ABC中，∠C＝90°，AC＝2，BC＝1，求tan∠A的值；小明想构造包含∠A的直角三角形：延长CA至D，使得DA＝AB，连接BD，所以得到∠D＝∠A，即转化为求∠D的正切值．

请按小明的思路进行余下的求解：

（3）拓展延伸：如图2，在Rt△ABC中，∠C＝90°，AC＝3，tanA＝．

①tan2A＝　 　；

②求tan3A的值．

Answer 1

【答案】（1），，≠；（2）﹣2；（3）①；②.

【解析】

（1）直接利用特殊角的三角函数值得结论；

（2）根据题意，利用勾股定理求AC，得结论；

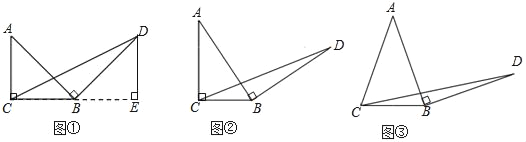
（3）①作AB的垂直平分线交AC于E，连接BE，则∠BEC=2∠A，在Rt△EBC中，利用勾股定理求出EC，求tan∠BEC得结果；

②作BM交AC于点M，使∠MBE=∠EBA，则∠BMC=3∠A．利用角平分线的性质和勾股定理求出EM的长，求tan∠BMC得结果.

（1）tan60°＝，tan30°＝，

发现结论：tanA≠2tan∠A，

故答案为：，，≠；

（2）在Rt△ABC中，∠C＝90°，AC＝2，BC＝1，

∴AB＝＝，

如图1，延长CA至D，使得DA＝AB，

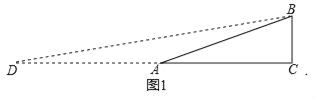
∴AD＝AB＝，

∴∠D＝∠ABD，

∴∠BAC＝2∠D，CD＝AD+AC＝2+，

∴tan∠A＝tan∠D＝＝﹣2；

（3）①如图2，作AB的垂直平分线交AC于E，连接BE，

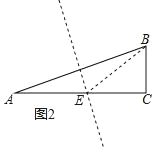
则∠BEC＝2∠A，AE＝BE，∠A＝∠ABE

∵Rt△ABC中，∠C＝90°，AC＝3，tanA＝，

∴BC＝1，AB＝，

设AE＝x，则EC＝3﹣x，

在Rt△EBC中，x2＝（3﹣x）2+1，

解得x＝，即AE＝BE＝，EC＝，

∴tan2A＝tan∠BEC＝＝，

故答案为：；

②如图3，作BM交AC于点M，使∠MBE＝∠EBA，

则∠BMC＝∠A+∠MBA＝3∠A．

设EM＝y，则MC＝EC﹣EM＝﹣y，

∵∠MBE＝∠EBA，

∴，即，

∴BM＝y，

在Rt△MBC中，BM2＝CM2+BC2

即（y）2＝（﹣y）2+1，

整理，得117y2+120y﹣125＝0，

解得，y1＝，y2＝﹣（不合题意，舍去）

即EM＝，CM＝﹣＝，

∴tan3A＝tan∠BMC＝，

＝＝．