Question

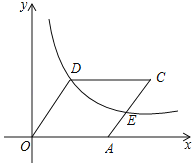
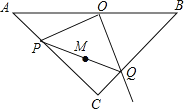
【题目】如图，等腰Rt△ABC中，斜边AB的长为2，O为AB的中点，P为AC边上的动点，OQ⊥OP交BC于点Q，M为PQ的中点，当点P从点A运动到点C时，点M所经过的路线长为（　　）

A. B. C. 1 D. 2

Answer 1

【答案】C

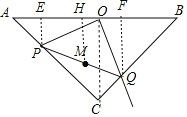
【解析】连接OC，作PE⊥AB于E，MH⊥AB于H，QF⊥AB于F，如图，利用等腰直角三角形的性质得AC=BC=，∠A=∠B=45°，OC⊥AB，OC=OA=OB=1，∠OCB=45°，再证明Rt△AOP≌△COQ得到AP=CQ，接着利用△APE和△BFQ都为等腰直角三角形得到PE=AP=CQ，QF=BQ，所以PE+QF=BC=1，然后证明MH为梯形PEFQ的中位线得到MH=，即可判定点M到AB的距离为，从而得到点M的运动路线为△ABC的中位线，最后利用三角形中位线性质得到点M所经过的路线长．

连接OC，作PE⊥AB于E，MH⊥AB于H，QF⊥AB于F，如图，

∵△ACB为到等腰直角三角形，

∴AC=BC=AB=，∠A=∠B=45°，

∵O为AB的中点，

∴OC⊥AB，OC平分∠ACB，OC=OA=OB=1，

∴∠OCB=45°，

∵∠POQ=90°，∠COA=90°，

∴∠AOP=∠COQ，

在Rt△AOP和△COQ中

，

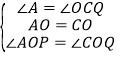∴Rt△AOP≌△COQ，

∴AP=CQ，

易得△APE和△BFQ都为等腰直角三角形，

∴PE=AP=CQ，QF=BQ，

∴PE+QF=（CQ+BQ）=BC==1，

∵M点为PQ的中点，

∴MH为梯形PEFQ的中位线，

∴MH=（PE+QF）=，

即点M到AB的距离为，

而CO=1，

∴点M的运动路线为△ABC的中位线，

∴当点P从点A运动到点C时，点M所经过的路线长=AB=1，

故选C．