题目内容
3.解不等式(组)(1)3-(x-1)>x-4(把解表示在数轴上)

(2)$\left\{\begin{array}{l}{\frac{1-x}{3}<1①}\\{5(x+1)≤2x+14②}\end{array}\right.$.
分析 (1)根据解不等式的基本步骤依次求解可得;
(2)分别求出每个不等式的解集即可得.
解答 解:(1)3-x+1>x-4,
-2x>-8,
x<4,
解集表示的数轴上如下:
(2)解不等式①得:x>-2,
解不等式②得:x≤3,
∴不等式组的解集为-2<x≤3.
点评 本题主要考查解一元一次不等式和不等式组,熟练掌握解不等式的基本步骤和不等式的性质是解题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
13. 如图,△ABC≌△DEF,∠A=85°,∠B=60°,则∠F的度数为( )
如图,△ABC≌△DEF,∠A=85°,∠B=60°,则∠F的度数为( )
 如图,△ABC≌△DEF,∠A=85°,∠B=60°,则∠F的度数为( )
如图,△ABC≌△DEF,∠A=85°,∠B=60°,则∠F的度数为( )| A. | 85° | B. | 60° | C. | 55° | D. | 35° |
15.若二次根式$\sqrt{3x-2}$无意义,则x的取值为( )
| A. | x≥$\frac{2}{3}$ | B. | x>$\frac{2}{3}$ | C. | x<$\frac{2}{3}$ | D. | x≤$\frac{2}{3}$ |
12.下列各式中,不是整式的是( )
| A. | 6xy | B. | $\frac{y}{x}$ | C. | x+9 | D. | 4 |
 如图,数学活动小组来到校园内的一盏路灯下测量路灯的高度,测角仪CE的高度为1.5米,测得仰角α为36°,点E到电灯杆底端D的距离DE为4米,求路灯的高度AD是多少米(结果精确到0.01)?(参考数据:sin36°≈0.588,cos36°≈0.809,tan36°≈0.727)
如图,数学活动小组来到校园内的一盏路灯下测量路灯的高度,测角仪CE的高度为1.5米,测得仰角α为36°,点E到电灯杆底端D的距离DE为4米,求路灯的高度AD是多少米(结果精确到0.01)?(参考数据:sin36°≈0.588,cos36°≈0.809,tan36°≈0.727) 如图,在△ABC中,
如图,在△ABC中,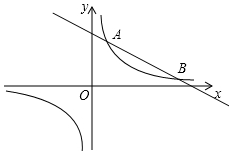 如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).