题目内容
17. 如图所示,在?ABCD中,E、F分别为AD、BC的中点,CE、AF分别交BD于M、N.求证:BN=MN=DM.
如图所示,在?ABCD中,E、F分别为AD、BC的中点,CE、AF分别交BD于M、N.求证:BN=MN=DM.
分析 由平行四边形的性质得出AD∥BC,AD=BC,再由已知条件得出AE∥CF,AE=CF,证出四边形AECF是平行四边形,得出CE∥AF,证出EM是△DAN的中位线,FN是△BCM的中位线,得出DM=MN,BN=MN,即可得出结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵E、F分别为AD、BC的中点,
∴AE=DE=$\frac{1}{2}$AD,CF=BF=$\frac{1}{2}$BC,
∴AE∥CF,AE=CF,
∴四边形AECF是平行四边形,
∴CE∥AF,
∴EM是△DAN的中位线,FN是△BCM的中位线,
∴DM=MN,BN=MN,
∴BN=MN=DM.
点评 本题考查了平行四边形的性质与判定、三角形中位线定理;熟练掌握平行四边形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
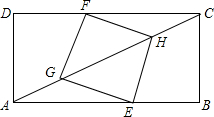 如图,矩形ABD中,AB=8,BC=4,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形.
如图,矩形ABD中,AB=8,BC=4,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形. 如图,点P是△ABC内一点,连接BP,并延长交AC于点D.
如图,点P是△ABC内一点,连接BP,并延长交AC于点D.
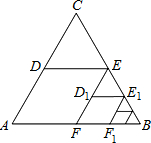 如图,△ABC是边长为1的等边三角形,取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的周长记作C1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的周长记作C2.照此规律作下去,则C2015=$\frac{1}{{2}^{2013}}$.
如图,△ABC是边长为1的等边三角形,取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的周长记作C1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的周长记作C2.照此规律作下去,则C2015=$\frac{1}{{2}^{2013}}$.