Question

如图，AB是⊙P的直径，弦CD∥AB，过点B的切线交AD的延长线于E，连接AC并延长至F，使CF=AC，连接EF．试判断AF与EF的位置关系．

Answer 1

考点：圆的综合题

专题：

分析：先连接BC，交AE于G，由于AB是直径，可知∠ACB=90°，根据AB∥CD，可得∠1=∠3，再根据同圆中同弧所对是圆周角相等，可得∠1=∠2，等量代换就有∠2=∠3，利用等角对等边可得GA=GB，又知BE是切线，那么∠ABE=90°，于是∠2+∠AEB=90°，∠3+∠GBE=90°，易证∠GEB=∠GBE，于是GE=GB，从而有AG=GE，再结合CF=AC，可知CG是△AEF的中位线，根据中位线性质可得BC∥EF，从而∠AFE=∠ACB=90°，即AF⊥EF．

解答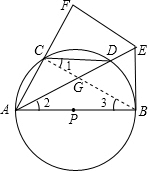：解：AF⊥EF．
连接BC，交AE于G，如右图，
∵AB是直径，
∴∠ACB=90°，
∵AB∥CD，
∴∠1=∠3，
∵∠1=∠2，
∴∠2=∠3，
∴AG=BG，
∵BE是切线，
∴∠ABE=90°，
∴∠2+∠AEB=90°，∠3+∠GBE=90°，
∴∠GEB=∠GBE，
∴GE=GB，
∴AG=GE，
又∵AC=CF，
∴CG是△AEF的中位线，
∴BC∥EF，
∴∠AFE=∠ACB=90°，
即AF⊥EF．

点评：本题是圆的综合题，解题的关键是作辅助线，构造直角三角形和平行线，并证明CG是△AEF的中位线．