题目内容
11. 如图,正方形ABCD中,E为BC的中点,F在CD上,且AF=BC+CF,求证:AE平分∠BAF.
如图,正方形ABCD中,E为BC的中点,F在CD上,且AF=BC+CF,求证:AE平分∠BAF.
分析 延长AE交DC的延长线于G,由正方形的性质得出∠B=∠BCD=∠ECG=90°,AB=BC,证明△GCE≌△ABE,得出GC=AB,∠G=∠BAE,证出AF=GF,得出∠FAE=∠G,得出∠FAE=∠BAE即可.
解答 证明:延长AE交DC的延长线于G,如图所示: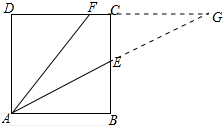 ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴∠B=∠BCD=∠ECG=90°,AB=BC,
∵E是BC的中点,
∴CE=BE,
在△GCE和△ABE中,$\left\{\begin{array}{l}{∠ECG=∠B}&{\;}\\{CE=BE}&{\;}\\{∠CEG=∠BEA}&{\;}\end{array}\right.$,
∴△GCE≌△ABE(ASA),
∴GC=AB,∠G=∠BAE,
∵AF=BC+CF,GF=GC+CF,
∴AF=GF,
∴∠FAE=∠G,
∴∠FAE=∠BAE,
∴AE平分∠BAF.
点评 本题考查了正方形的性质、全等三角形的判定与性质、等腰三角形的性质;熟练掌握正方形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
1.图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,…,则第⑦个图形棋子的个数为( )
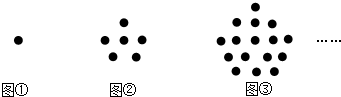

| A. | 76 | B. | 96 | C. | 106 | D. | 116 |
3. 如图,将?ABCD绕点C顺时针旋转一定角度后,得到?EFCG,若BC与CG在同一直线上,点D在EG上,则旋转的度数为( )
如图,将?ABCD绕点C顺时针旋转一定角度后,得到?EFCG,若BC与CG在同一直线上,点D在EG上,则旋转的度数为( )
 如图,将?ABCD绕点C顺时针旋转一定角度后,得到?EFCG,若BC与CG在同一直线上,点D在EG上,则旋转的度数为( )
如图,将?ABCD绕点C顺时针旋转一定角度后,得到?EFCG,若BC与CG在同一直线上,点D在EG上,则旋转的度数为( )| A. | 45° | B. | 50° | C. | 45° | D. | 60° |
 如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF,请回答下列问题:
如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF,请回答下列问题: