题目内容
⊙O的半径为1,弦AB= ,弦AC=
,弦AC= ,则∠CAB的度数为
,则∠CAB的度数为
- A.15°
- B.30°
- C.45°
- D.15°或75°
D
分析:首先根据题意画出图形,注意分为弦AB与弦AC在圆心的同侧与异侧,然后连接OA,OB,过点O作OD⊥AC于D,由垂径定理,可求得AD的长,然后由勾股定理的逆定理,可判定△AOB是等腰直角三角形,则可求得∠BAO的度数,由三角函数可求得∠OAD的度数,继而求得答案.
解答: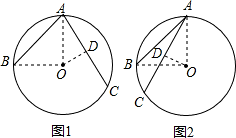 解:如图1,连接OA,OB,过点O作OD⊥AC于D,
解:如图1,连接OA,OB,过点O作OD⊥AC于D,
∵⊙O的半径为1,弦AB= ,弦AC=
,弦AC= ,
,
∴OA=OB=1,AD= AC=
AC= ,
,
∴OA2+OB2=AB2,
∴∠AOB=90°,
∴∠BAO=45°,
在Rt△AOD中,cos∠OAD= =
= ,
,
∴∠OAD=30°,
∴∠BAC=∠BAO+∠OAD=75°;
如图2,连接OA,OB,过点O作OD⊥AC于D,
∵⊙O的半径为1,弦AB= ,弦AC=
,弦AC= ,
,
∴OA=OB=1,AD= AC=
AC= ,
,
∴OA2+OB2=AB2,
∴∠AOB=90°,
∴∠BAO=45°,
在Rt△AOD中,cos∠OAD= =
= ,
,
∴∠OAD=30°,
∴∠BAC=∠BAO-∠OAD=15°.
∴∠CAB的度数为:75°或15°.
故选D.
点评:此题考查了垂径定理、勾股定理的逆定理以及三角函数等知识.此题难度适中,注意掌握数形结合思想与分类讨论思想的应用.
分析:首先根据题意画出图形,注意分为弦AB与弦AC在圆心的同侧与异侧,然后连接OA,OB,过点O作OD⊥AC于D,由垂径定理,可求得AD的长,然后由勾股定理的逆定理,可判定△AOB是等腰直角三角形,则可求得∠BAO的度数,由三角函数可求得∠OAD的度数,继而求得答案.
解答:
 解:如图1,连接OA,OB,过点O作OD⊥AC于D,
解:如图1,连接OA,OB,过点O作OD⊥AC于D,∵⊙O的半径为1,弦AB=
 ,弦AC=
,弦AC= ,
,∴OA=OB=1,AD=
 AC=
AC= ,
,∴OA2+OB2=AB2,
∴∠AOB=90°,
∴∠BAO=45°,
在Rt△AOD中,cos∠OAD=
 =
= ,
,∴∠OAD=30°,
∴∠BAC=∠BAO+∠OAD=75°;
如图2,连接OA,OB,过点O作OD⊥AC于D,
∵⊙O的半径为1,弦AB=
 ,弦AC=
,弦AC= ,
,∴OA=OB=1,AD=
 AC=
AC= ,
,∴OA2+OB2=AB2,
∴∠AOB=90°,
∴∠BAO=45°,
在Rt△AOD中,cos∠OAD=
 =
= ,
,∴∠OAD=30°,
∴∠BAC=∠BAO-∠OAD=15°.
∴∠CAB的度数为:75°或15°.
故选D.
点评:此题考查了垂径定理、勾股定理的逆定理以及三角函数等知识.此题难度适中,注意掌握数形结合思想与分类讨论思想的应用.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
⊙O的半径为5cm,弦AB∥CD,且AB=6cm,CD=8cm,则AB与CD之间的距离为( )
| A、1cm | B、7cm | C、3cm或4cm | D、1cm或7cm |
 如图,一种花边是由弓形组成的,
如图,一种花边是由弓形组成的, |
| ACB |
| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
 如图,⊙O的半径为5,弦AB=8,OC⊥AB于C,则OC的长等于
如图,⊙O的半径为5,弦AB=8,OC⊥AB于C,则OC的长等于 如图,⊙O的半径为2,弦AB=
如图,⊙O的半径为2,弦AB=