题目内容
5.某超市在五十天内试销一款成本为40元/件的新型商品,此款商品在第x天的销售量p(件)与销售的天数x的关系为p=120-2x,销售单价q(元/件)与x满足:当1≤x<25时,q=x+60;当25≤x≤50时,q=40+$\frac{1125}{x}$.(1)求该超市销售这款商品第x天获得的利润y(元)关于x的函数关系式;
(2)这五十天,该超市第几天获得的利润最大?最大利润为多少?
分析 (1)根据y=p(q-40),根据1≤x<25时,q=x+60;25≤x≤50时,q=40+$\frac{1125}{x}$分别代入可得;
(2)根据二次函数的性质和反比例函数的性质分别求得最大值,比较可得.
解答 解:(1)y=p(q-40),
当1≤x<25时,y=(120-2x)(x+60-40)=-2x2+80x+2400;
当25≤x≤50时,y=(120-2x)(40+$\frac{1125}{x}$-40)=$\frac{135000}{x}$-2250;
(2)当1≤x<25时,y=-2x2+80x+2400=-2(x-20)2+3200,
∴当x=20时,y取得最大值3200;
当25≤x≤50时,y=$\frac{135000}{x}$-2250,
当x=25时,y取得最大值为3150;
答:该超市第20天获得的利润最大,最大利润为3200元.
点评 本题主要考查二次函数的应用与反比例函数的应用,根据题意得出y关于x的函数解析式及熟练掌握函数的性质是解题的关键.

练习册系列答案
相关题目
16.4的倒数是( )
| A. | 4 | B. | -4 | C. | $\frac{1}{4}$ | D. | -$\frac{1}{4}$ |
20. 如图,AB是⊙O的直径,过⊙O上的点作⊙O的切线,交AB的延长线于点D,若∠A=25°,则∠D的大小是( )
如图,AB是⊙O的直径,过⊙O上的点作⊙O的切线,交AB的延长线于点D,若∠A=25°,则∠D的大小是( )
 如图,AB是⊙O的直径,过⊙O上的点作⊙O的切线,交AB的延长线于点D,若∠A=25°,则∠D的大小是( )
如图,AB是⊙O的直径,过⊙O上的点作⊙O的切线,交AB的延长线于点D,若∠A=25°,则∠D的大小是( )| A. | 25° | B. | 40° | C. | 50° | D. | 65° |
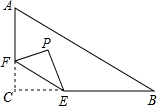 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点F在边AC上,并且CF=1,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是$\frac{3}{5}$.
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点F在边AC上,并且CF=1,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是$\frac{3}{5}$.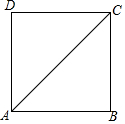 如图,正方形ABCD的对角线AC长为2$\sqrt{2}$,若直线满足:①点C到直线l的距离为1;②B、D两点到直线l的距离相等,那么符合题意的直线l有4条.
如图,正方形ABCD的对角线AC长为2$\sqrt{2}$,若直线满足:①点C到直线l的距离为1;②B、D两点到直线l的距离相等,那么符合题意的直线l有4条.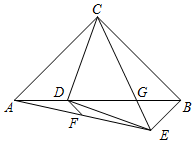 如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D为边AB上一点,CD绕点D顺时针旋转90°至DE,CE交AB于点G.已知AD=8,BG=6,点F是AE的中点,连接DF,求线段DF的长2$\sqrt{2}$.
如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D为边AB上一点,CD绕点D顺时针旋转90°至DE,CE交AB于点G.已知AD=8,BG=6,点F是AE的中点,连接DF,求线段DF的长2$\sqrt{2}$.