题目内容
如图,在△ABC的AB、AC边的外侧作等边△ACE和等边△ABF,连接BE、CF相交于 点O,
点O,
(1)求证:CF=BE;
(2)连AO,则:①AO平分∠BAC;②OA平分∠EOF,你认为正确的是
 点O,
点O,(1)求证:CF=BE;
(2)连AO,则:①AO平分∠BAC;②OA平分∠EOF,你认为正确的是
②
②
(填①或②).并证明你的结论.分析:(1)根据等边三角形的性质得到AB=AF,AC=AE,∠FAB=∠EAC=60°,则∠FAC=∠BAE,易证得△ABE≌△AFC,即可得到结论;
(2)连AO,过A分别作AP⊥CF与P,AQ⊥BE于Q,由(1)得△ABE≌△AFC,得到S△ABE=S△AFC,则AP=AQ,则OA不一定平分∠MAN,进而得出RT△AOP≌RT△AOM,则OA平分∠EOF.
(2)连AO,过A分别作AP⊥CF与P,AQ⊥BE于Q,由(1)得△ABE≌△AFC,得到S△ABE=S△AFC,则AP=AQ,则OA不一定平分∠MAN,进而得出RT△AOP≌RT△AOM,则OA平分∠EOF.
解答:(1)证明:∵△ABF和△ACE是等边三角形,
∴AB=AF,AC=AE,∠FAB=∠EAC=60°,
∴∠FAB+∠BAC=∠EAC+∠BAC,
即∠FAC=∠BAE,
在△ABE与△AFC中,
AB=AF
∠BAE=FAC
AE=AC
∴△ABE≌△AFC(SAS),
∴BE=FC;
(2)解:连AO,过A分别作AP⊥CF与P,AM⊥BE于Q,如图,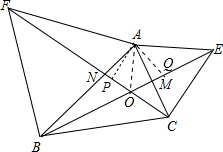
∵△ABE≌△AFC,
∴S△ABE=S△AFC,
∴
AP•CF=
AQ•BE,
而CF=BE,
∴AP=AQ,
∴OA不一定平分∠MAN,所以①错误;
∵在RT△AOP和RT△AOM中,
,
∴RT△AOP≌RT△AOM(HL)
∴∠AOF=∠AOE,所以②正确.
故答案为②.
∴AB=AF,AC=AE,∠FAB=∠EAC=60°,
∴∠FAB+∠BAC=∠EAC+∠BAC,
即∠FAC=∠BAE,
在△ABE与△AFC中,
AB=AF
∠BAE=FAC
AE=AC
∴△ABE≌△AFC(SAS),
∴BE=FC;
(2)解:连AO,过A分别作AP⊥CF与P,AM⊥BE于Q,如图,

∵△ABE≌△AFC,
∴S△ABE=S△AFC,
∴
| 1 |
| 2 |
| 1 |
| 2 |
而CF=BE,
∴AP=AQ,
∴OA不一定平分∠MAN,所以①错误;
∵在RT△AOP和RT△AOM中,
|
∴RT△AOP≌RT△AOM(HL)
∴∠AOF=∠AOE,所以②正确.
故答案为②.
点评:本题考查了全等三角形的判定与性质:如果两边对应相等,且它们的夹角相等,那么这两个三角形全等;全等三角形的对应边相等,对应角相等.也考查了等边三角形的性质以及四点共圆的性质和判定.

练习册系列答案
相关题目
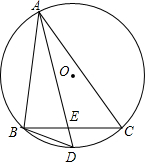 如图,在△ABC的外接圆O中,D是弧BC的中点,AD交BC于点E,连接BD.连接DC,DC2=DE•DA是否成立?若成立,给出证明;若不成立,举例说明.
如图,在△ABC的外接圆O中,D是弧BC的中点,AD交BC于点E,连接BD.连接DC,DC2=DE•DA是否成立?若成立,给出证明;若不成立,举例说明.

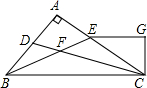 如图,在△ABC的角平分线CD,BE相交于F,∠A=90°,EG∥BC,且EG⊥CG于G,下列说法:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ACG=∠ABC;④∠DFB=
如图,在△ABC的角平分线CD,BE相交于F,∠A=90°,EG∥BC,且EG⊥CG于G,下列说法:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ACG=∠ABC;④∠DFB=