题目内容
已知过P(0,1)的直线与y=x2交于A、B两点,S△AOB=3
.求直线AB的解析式.
| 2 |
考点:二次函数的性质,待定系数法求一次函数解析式
专题:计算题
分析:设直线AB的解析式为y=kx+1,由两解析式组成方程组后消去y得到关于x的方程x2-kx-1=0,解得x1=
,x2=
,于是得到两交点的横坐标,再利用S△AOB=S△OAP+S△OBP=3
可得到关于k的方程,然后解方程即可.
k+
| ||
| 2 |
k-
| ||
| 2 |
| 2 |
解答:解:如图,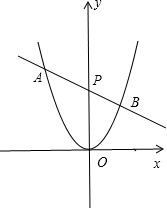
设直线AB的解析式为y=kx+1,
,消去y得到x2-kx-1=0,
所以x1=
,x2=
,
即点A、B的横坐标分别为
和
,
所以S△AOB=S△OAP+S△OBP=3
,
即
•(-
)•1+
•
•1=3
,
解得k=±2
,
所以直线AB的解析式为y=2
x+1或y=-2
x+1.

设直线AB的解析式为y=kx+1,
|
所以x1=
k+
| ||
| 2 |
k-
| ||
| 2 |
即点A、B的横坐标分别为
k+
| ||
| 2 |
k-
| ||
| 2 |
所以S△AOB=S△OAP+S△OBP=3
| 2 |
即
| 1 |
| 2 |
k-
| ||
| 2 |
| 1 |
| 2 |
k+
| ||
| 2 |
| 2 |
解得k=±2
| 71 |
所以直线AB的解析式为y=2
| 71 |
| 71 |
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 在四边形ABCD中,∠ADC+∠ABC=90°,AD=CD=
在四边形ABCD中,∠ADC+∠ABC=90°,AD=CD=