题目内容
2.如图1,已知在平面直角坐标系中,抛物线y=ax2+bx+3经过A(-1,0),B(3,0)两点,且与y轴交于点C.(1)求抛物线的解析式及顶点D的坐标;
(2)设△COB沿x轴正方向平移t(0<t≤3)个单位长度时,△COB与△CDB重叠部分的面积为S,求S与t之间的函数关系式,并指出t的取值范围;
考生请注意:下面的(3),(4),(5)题为三选一的选做题,即只能选做其中一个题目,多答时只按作答的首题评分,切记哟!
(3)点P是x轴上的一个动点,过点P作直线l∥AC交抛物线与点Q,试探究:随着P点的运动,在抛物线上是否存在点Q,使以点A、P、Q、C为顶点的四边形是平行四边形?若存在,请直接写出符合条件的点Q的坐标;若不存在,请说明理由;
(4)设点Q是y轴右侧抛物线上异于点B的点,过点Q做QP∥x轴交抛物线于另一点P,过P做PH⊥x轴,垂足为H,过Q做QG⊥x轴,垂足为G,则四边形QPHG为矩形.试探究在点Q运动的过程中矩形QPHG能否成为正方形?若能,请直接写出符合条件的点Q的坐标;若不能,请说明理由;
(5)试探究,在y轴右侧的抛物线上是否存在一点Q,使△QDC是等腰三角形?若存在,请直接写出符合条件的点Q坐标;若不存在,请说明理由.
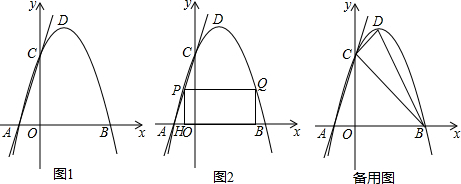
分析 (1)已知A、B的坐标,利用待定系数法可确定抛物线的解析式,进而能得到顶点D的坐标;
(2)过C作CF∥x轴交BD于F,当C点运动在CF之间时,△COB与△CDB重叠部分是个四边形;当C点运动到F点右侧时,△COB与△CDB重叠部分是个三角形.按上述两种情况按图形之间的和差关系进行求解;
(3)分点P在点Q的左边和右边两种情况,根据平行四边形的对边平行且相等,从点A、C的坐标关系,用点P的坐标表示出点Q的坐标,然后把点Q的坐标代入抛物线解析式求解即可;
(4)表示出PQ和BQ的长,列方程求解即可;
(5)求出D的坐标和对称轴的表达式,分为两种情况:①若以CD为底边,则QC=QD.设Q点坐标为(a,b),根据勾股定理求出b=4-a,代入抛物线求出a、b,②若以CD为一腰,根据抛物线对称性得出点Q与点C关于直线x=1对称,即可求出Q的坐标.
解答 解:(1)∵抛物线y=ax2+bx+3经过A(-1,0),B(3,0)两点,
∴$\left\{\begin{array}{l}{a-b+3=0}\\{9a+3b+3=0}\end{array}\right.$
解得:a=-1,b=2,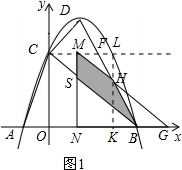
∴y=-x2+2x+3
∵y=-x2+2x+3=-(x-1)2+4,
∴顶点D的坐标为(1,4);
(2)设直线AB的解析式为y=kx+b.
将B(3,0),D(1,4)代入,
得$\left\{\begin{array}{l}{3k+b=0}\\{k+b=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-2}\\{b=6}\end{array}\right.$
∴y=-2x+6.
过点C作射线CF∥x轴交BD于点F,当y=3时,得x=$\frac{3}{2}$,
∴F($\frac{3}{2}$,3).
情况一:如图1,当0<t≤$\frac{3}{2}$时,设△COB平移到△GNM的位置,MG交BD于点H,MN交BC于点S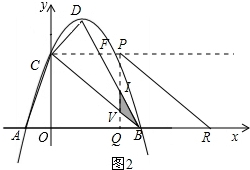
则ON=BG=t,过点H作LK⊥x轴于点K,交EF于点L.
由△BHG∽△FHM,得$\frac{BG}{FM}=\frac{HK}{HL}$,
即$\frac{t}{\frac{3}{2}-t}=\frac{HK}{3-HK}$,解得HK=2t.
∴S阴=S△MNG-S△SNB-S△HBG=$\frac{1}{2}$×3×3-$\frac{1}{2}$(3-t)2-$\frac{1}{2}$t•2t=-$\frac{3}{2}$t2+3t;
情况二:如图2,当$\frac{3}{2}$<t≤3时,设△AOE平移到△PQR的位置,PQ交AB于点I,交AE于点V.
由△IQB∽△IPF,得$\frac{BQ}{FP}=\frac{IQ}{IP}$,
即$\frac{3-t}{t-\frac{3}{2}}=\frac{IQ}{3-IQ}$,解得IQ=2(3-t).
∵BQ=VQ=3-t,
∴S阴=$\frac{1}{2}$IV•BQ=$\frac{1}{2}$(3-t)2=$\frac{1}{2}$t2-3t+$\frac{9}{2}$.
综上所述:s=$\left\{\begin{array}{l}{-\frac{3}{2}{t}^{2}+3t(0<t≤\frac{3}{2})}\\{\frac{1}{2}{t}^{2}-3t+\frac{9}{2}(\frac{3}{2}<t≤3)}\end{array}\right.$;
(3)存在,
∵直线l∥AC,
∴PQ∥AC且PQ=AC,
∵A(-1,0),C(0,3),
∴设点P的坐标为(x,0),
则①若点Q在x轴上方,则点Q的坐标为(x+1,3),
此时,-(x+1)2+2(x+1)+3=3,
解得x1=-1(舍去),x2=1,
所以,点Q的坐标为(2,3),
②若点Q在x轴下方,则点Q的坐标为(x-1,-3),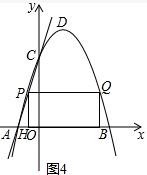
此时,-(x-1)2+2(x-1)+3=-3,
整理得,x2-4x-3=0,
解得x1=2+$\sqrt{7}$,x2=2-$\sqrt{7}$,
所以,点Q的坐标为(1+$\sqrt{7}$,-3)或(1-$\sqrt{7}$,-3),
综上所述,点Q的坐标为(2,3)或(1+$\sqrt{7}$,-3)或(1-$\sqrt{7}$,-3);
(4)存在,
点Q的坐标为(x,-x2+2x+3),
∵P、Q是抛物线上一对对称点,对称轴为x=1,
∴p(2-x,-x2+2x+3)
∵四边形QPHG为矩形,
∴当PQ=BQ时,四边形QPHG为正方形,
∴x-(2-x)=-x2+2x+3,
解得:x=$\sqrt{5}$或x=-$\sqrt{5}$(不合题意舍去),
当x=$\sqrt{5}$时,y=-x2+2x+3=-5+2$\sqrt{5}$+3=2$\sqrt{5}$-2,
∴当Q的坐标为($\sqrt{5}$,2$\sqrt{5}$-2)时,四边形QPHG为正方;
(5)存在.
由y=-x2+2x+3=-(x-1)2+4知,D点坐标为(1,4),对称轴为x=1,
①若以CD为底边,则PC=PD.设P点坐标为(a,b),
由勾股定理,得:a2+(3-b)2=(a-1)2+(4-b)2,
即b=4-a.
又点P(a,b)在抛物线上,b=-a2+2a+3,
则 4-a=-a2+2a+3.整理,得a2-3a+1=0,
解,得a=存在.
由y=-x2+2x+3=-(x-1)2+4知,D点坐标为(1,4),对称轴为x=1,
①若以CD为底边,则PC=PD.设P点坐标为(a,b),
由勾股定理,得:a2+(3-b)2=(a-1)2+(4-b)2,
即b=4-a.
又点P(a,b)在抛物线上,b=-a2+2a+3,
则 4-a=-a2+2a+3.整理,得a2-3a+1=0,
解,得a=$\frac{3+\sqrt{5}}{2}$>0或a=$\frac{3-\sqrt{5}}{2}$<0(不合题意舍去),
则b=4-$\frac{3+\sqrt{5}}{2}$=$\frac{5-\sqrt{5}}{2}$,
∴Q($\frac{3+\sqrt{5}}{2}$,$\frac{5-\sqrt{5}}{2}$);
②若以CD为一腰,因点P在对称轴右侧的抛物线上,由抛物线对称性知,点P与点C关于直线x=1对称,
此时点P坐标为(2,3),
综上所述,符合条件的点P坐标为Q($\frac{3+\sqrt{5}}{2}$,$\frac{5-\sqrt{5}}{2}$)或(2,3).
点评 本题考查了用待定系数法求抛物线的解析式,二次函数的顶点坐标,勾股定理,三角形相似的判定与性质,三角形面积计算,平行四边形的对边平行且相等的性质,正方形的判定和性质,等腰三角形的判定等知识点的运用,培养学生运用性质进行计算的能力,用的数学思想是分类讨论思想,题目综合性比较强,有一定的难度.

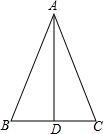 如图,在△ABC中,AB=AC,AD是边BC上的高,求证:
如图,在△ABC中,AB=AC,AD是边BC上的高,求证: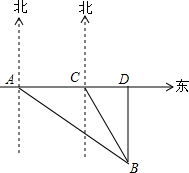 如图,新城区新建了三个商业城A,B,C,其中C在A的正东方向,在A处测得B在A的南偏东52°的方向,在C处测得B在C的南偏东26°的方向,已知A和B的距离是1000m.现有甲、乙两个工程对修建道路,甲修建一条从A到C的笔直道路AC,乙修建一条从B到直线AC最近的道路BD.求甲、乙修建的道路各是多长.(结果精确到1m)(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)
如图,新城区新建了三个商业城A,B,C,其中C在A的正东方向,在A处测得B在A的南偏东52°的方向,在C处测得B在C的南偏东26°的方向,已知A和B的距离是1000m.现有甲、乙两个工程对修建道路,甲修建一条从A到C的笔直道路AC,乙修建一条从B到直线AC最近的道路BD.求甲、乙修建的道路各是多长.(结果精确到1m)(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,sin64°≈0.90,cos64°≈0.44,tan64°≈2.05) 一个工件,外部是圆柱体,内部凹槽是正方体,如图所示,其中,正方体一个面的四个顶点都在圆柱底面的圆周上,若圆柱底面周长为2πcm,则正方体的体积为2$\sqrt{2}$cm3.
一个工件,外部是圆柱体,内部凹槽是正方体,如图所示,其中,正方体一个面的四个顶点都在圆柱底面的圆周上,若圆柱底面周长为2πcm,则正方体的体积为2$\sqrt{2}$cm3. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论: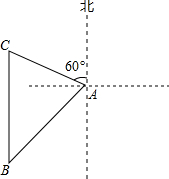 如图,海中一小岛上有一个观测点A,某天上午9:00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.当天上午9:30观测到该渔船在观测点A的北偏西60°方向上的C处.若该渔船的速度为每小时30海里,在此航行过程中,问该渔船从B处开始航行多少小时,离观测点A的距离最近?(计算结果用根号表示,不取近似值).
如图,海中一小岛上有一个观测点A,某天上午9:00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.当天上午9:30观测到该渔船在观测点A的北偏西60°方向上的C处.若该渔船的速度为每小时30海里,在此航行过程中,问该渔船从B处开始航行多少小时,离观测点A的距离最近?(计算结果用根号表示,不取近似值).