题目内容
20.已知x=$\frac{\sqrt{5}-1}{2}$,y=$\frac{\sqrt{5}+1}{2}$,求$\frac{y}{x}$+$\frac{x}{y}$的值.分析 先由已知条件得出x+y=$\frac{2\sqrt{5}}{2}$=$\sqrt{5}$,xy=$\frac{5-1}{4}$=1,再将$\frac{y}{x}$+$\frac{x}{y}$变形为$\frac{(x+y)^{2}-2xy}{xy}$,整体代入即可求解.
解答 解:∵x+y=$\frac{2\sqrt{5}}{2}$=$\sqrt{5}$,xy=$\frac{5-1}{4}$=1,
∴$\frac{y}{x}$+$\frac{x}{y}$=$\frac{{y}^{2}+{x}^{2}}{xy}$=$\frac{(x+y)^{2}-2xy}{xy}$=$\frac{(\sqrt{5})^{2}-2×1}{1}$=3.
点评 考查了分母有理化,关键是由已知条件得出x+y=$\frac{2\sqrt{5}}{2}$=$\sqrt{5}$,xy=$\frac{5-1}{4}$=1,注意整体思想的运用.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
15.下列函数中,经过一、二、四象限的函数是( )
| A. | y=7 | B. | y=-2x | C. | y=-2x-7 | D. | y=-2x+7 |
12.某教育主管部门深入边远山区,随机走访农户,调查农村儿童生活教育现状,根据收集的数据编制了不完整的统计图表如下:
山区儿童生活教育现状
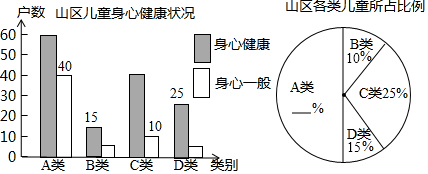
请你用学过的统计知识,解决问题:
(1)教育主管部门走访了边远山区多少家农户?
(2)将统计图表中的空缺数据填写完整;
(3)分析数据后,请你提一条合理建议.
山区儿童生活教育现状
| 类别 | 现状 | 户数 | 比例 |
| A类 | 父母长年在外打工,孩子留在老家由老人照顾 | 100 | |
| B类 | 父母长年在外打工,孩子带在身边 | 10% | |
| C类 | 父母就近在城镇打工,晚上回家照顾孩子 | 50 | |
| D类 | 父母在家务农,并照顾孩子 | 15% |

请你用学过的统计知识,解决问题:
(1)教育主管部门走访了边远山区多少家农户?
(2)将统计图表中的空缺数据填写完整;
(3)分析数据后,请你提一条合理建议.
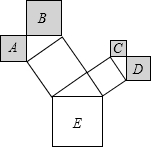 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别为2,4,1,2,则最大的正方形E的面积是9.
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别为2,4,1,2,则最大的正方形E的面积是9.