题目内容
当整数m=
0
0
时，直线y=2x-m+3与直线y=-x+2m的交点位于第二象限．分析：先解方程组得
确定直线y=2x-m+3与直线y=-x+2m的交点坐标为（m-1，m+1），再根据第二象限点的坐标特征得到-1＜m＜1，然后找出此范围内的整数即可．
|
解答：解：根据题意得
，解得
，
即直线y=2x-m+3与直线y=-x+2m的交点坐标为（m-1，m+1），
∵点（m-1，m+1）在第二象限，
∴
，
∴-1＜m＜1，
∴满足条件的整数m为0．
故答案为0．
|
|
即直线y=2x-m+3与直线y=-x+2m的交点坐标为（m-1，m+1），
∵点（m-1，m+1）在第二象限，
∴
|
∴-1＜m＜1，
∴满足条件的整数m为0．
故答案为0．
点评：本题考查了两条直线相交或平行问题：若直线y=k1x+b1与直线y=k2x+b2平行，则k1=k2；若直线y=k1x+b1与直线y=k2x+b2相交，则由两解析式所组成的方程组的解为交点坐标
练习册系列答案
相关题目
（与点B、C不重合），过N作直线MN⊥x轴，垂足为A，交DC边于M．设OA=t，△OMN的面积为s．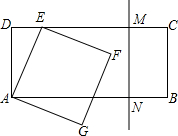
（2013•湖州二模）如图，矩形ABCD中，AB=8，AD=3．点E从D向C以每秒1个单位的速度运动，以AE为一边在AE的右下方作正方形AEFG．同时垂直于CD的直线MN也从C向D以每秒2个单位的速度运动，当经过多少秒时．直线MN和正方形AEFG开始有公共点？（ ）
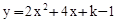（k为正整数）.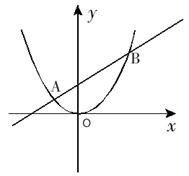
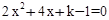（k为正整数）有两个不相等的整数解，点A（m，y1），B（m+1，y2），C（m+2，y3）都在二次函数