题目内容
13. 如图所示是某机械零件的平面图,尺寸如图所示,求两孔中心A,B之间的距离.(单位:毫米)
如图所示是某机械零件的平面图,尺寸如图所示,求两孔中心A,B之间的距离.(单位:毫米)
分析 根据题意可得AC与BC的取值,又由勾股定理,即可求得AB的值,即可求得两圆孔中心A和B的距离.
解答  解:如图,在△ABC中,∠ACB=90°,AC=35mm,BC=56mm,
解:如图,在△ABC中,∠ACB=90°,AC=35mm,BC=56mm,
由勾股定理,得:AB=$\sqrt{3{5}^{2}+5{6}^{2}}$=$\sqrt{4361}$(mm),
答:两圆孔中心A和B的距离为$\sqrt{4361}$mm.
点评 此题考查了勾股定理的应用.解此题的关键是注意数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.某公司2007年的利润是a万元,计划以后每年在前一年的基础上增长m%,则2010年的利润是( )
| A. | a(1+m%)2 | B. | a(1+m%)3 | C. | a(1+m%)4 | D. | (a+m%)3 |
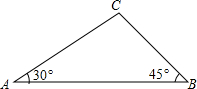 如图,在△ABC中,∠A=30°,∠B=45°,AC=2$\sqrt{3}$,则CB的长为$\sqrt{6}$.
如图,在△ABC中,∠A=30°,∠B=45°,AC=2$\sqrt{3}$,则CB的长为$\sqrt{6}$. 如图所示,在梯形ABCD中,DC∥AB,$\frac{DC}{AB}$=$\frac{1}{3}$,MN为中位线,EF∥AB且通过AC与BD的交点,点E,F分别在AD,BC上,则梯形CDEF,梯形FEMN,梯形NMAB面积的连比等于5:7:20.
如图所示,在梯形ABCD中,DC∥AB,$\frac{DC}{AB}$=$\frac{1}{3}$,MN为中位线,EF∥AB且通过AC与BD的交点,点E,F分别在AD,BC上,则梯形CDEF,梯形FEMN,梯形NMAB面积的连比等于5:7:20.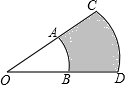 如图,两个同心圆被两条半径截得的$\widehat{AB}$=6πcm,$\widehat{CD}$=10πcm,且AC=12cm,求阴影部分ABDC的面积.
如图,两个同心圆被两条半径截得的$\widehat{AB}$=6πcm,$\widehat{CD}$=10πcm,且AC=12cm,求阴影部分ABDC的面积.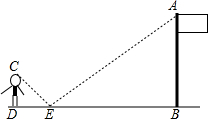 如图,在点E处水平放置一面镜子,人站在D处,恰好能看见旗杆的顶端A,测量眼睛C距地面的高度CD=1.65m,且人与镜子和旗杆底端的距离分别为DE=2m,DB=14.8m.请你计算出旗杆的高度.
如图,在点E处水平放置一面镜子,人站在D处,恰好能看见旗杆的顶端A,测量眼睛C距地面的高度CD=1.65m,且人与镜子和旗杆底端的距离分别为DE=2m,DB=14.8m.请你计算出旗杆的高度.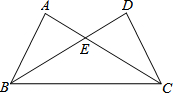 如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D=90°,AB=DC.
如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D=90°,AB=DC.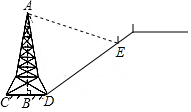 如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=24 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为28.8m.
如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=24 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为28.8m.