题目内容
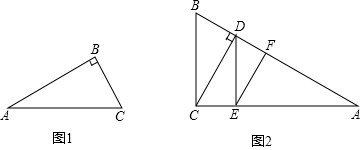
15. 已知:如图,在△ABC中,∠B>∠C,AE为∠BAC的平分线,AD⊥BC于点D.求证:∠DAE=$\frac{1}{2}$(∠B-∠C)
已知:如图,在△ABC中,∠B>∠C,AE为∠BAC的平分线,AD⊥BC于点D.求证:∠DAE=$\frac{1}{2}$(∠B-∠C)
分析 根据三角形内角和定理以及AD是BC边上的高,求得∠BAD=90°-∠B,再根据AE平分∠BAC,求得∠BAE=$\frac{1}{2}$∠BAC=$\frac{1}{2}$(180°-∠B-∠C)=90°-$\frac{1}{2}$∠B-$\frac{1}{2}$∠C,最后根据∠DAE=∠BAE-∠BAD即可求解.
解答 证明:∵AD是BC边上的高,
∴∠BAD=90°-∠B.
∵AE平分∠BAC,
∴∠BAE=$\frac{1}{2}$∠BAC=$\frac{1}{2}$(180°-∠B-∠C)=90°-$\frac{1}{2}$∠B-$\frac{1}{2}$∠C.
∵∠DAE=∠BAE-∠BAD,
∴∠DAE=(90°-$\frac{1}{2}$∠B-$\frac{1}{2}$∠C)-(90°-∠B)=$\frac{1}{2}$∠B-$\frac{1}{2}$∠C=$\frac{1}{2}$(∠B-∠C).
点评 本题考查三角形的内角和定理及角平分线的性质,高线的性质,解答的关键是三角形的内角和定理:三角形内角和是180°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
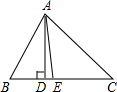
6. 如图,AC=BC=BD,AD=AE,DE=CE,则∠B为( )度.
如图,AC=BC=BD,AD=AE,DE=CE,则∠B为( )度.
 如图,AC=BC=BD,AD=AE,DE=CE,则∠B为( )度.
如图,AC=BC=BD,AD=AE,DE=CE,则∠B为( )度.| A. | 30° | B. | 36° | C. | 40° | D. | 45° |
4.下列抽样方法是随机抽样的是( )
| A. | 为了解刚生产的零件的质量情况,从每一个包装箱内抽5个加以检查 | |
| B. | 为了解全市学生的身高情况,以一、三中的学生为代表进行考察 | |
| C. | 为了解小学生的视力情况,选中六年级20名学生进行调查 | |
| D. | 为了解某地区的车流量,记录某一红绿灯处早上8:00至9:00的车流量 |
 桌面上放着两个物体,分别从它们的正面、左面、上面三个方向看到的图形如图,则这两个物体分别是长方体和圆柱,它们的位置是圆柱前长方体后.
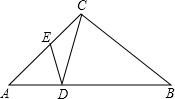
桌面上放着两个物体,分别从它们的正面、左面、上面三个方向看到的图形如图,则这两个物体分别是长方体和圆柱,它们的位置是圆柱前长方体后. 如图,△ABC中,E为BC的中点,DE⊥BC于E,交AC于D,△ABD的周长为21,AB=10,则AC=11.
如图,△ABC中,E为BC的中点,DE⊥BC于E,交AC于D,△ABD的周长为21,AB=10,则AC=11.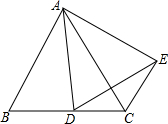 如图,△ABC是等边三角形,AD=AE,BD=CE,求∠ACE的度数.
如图,△ABC是等边三角形,AD=AE,BD=CE,求∠ACE的度数.