题目内容
如图,下面由火柴棒拼出的一系列的图形中,第n个图形由n个正方形组成.当n=2014时,火柴棒的根数是 .


考点:规律型:图形的变化类
专题:
分析:易得n=1时火柴的根数,分别求得n为任意值时,火柴的根数在4的基础上增加了几个3即可得到规律,代入n=2014即可求解.
解答:解:n=1时,有4根火柴;
n=2时,有4+3=7根火柴;
n=3时,有4+2×3=10根火柴;
…
s=4+(n-1)×3=3n+1,
当n=2014时,S=3×2014+1=6043,
故答案为:6043;
n=2时,有4+3=7根火柴;
n=3时,有4+2×3=10根火柴;
…
s=4+(n-1)×3=3n+1,
当n=2014时,S=3×2014+1=6043,
故答案为:6043;
点评:考查图形的规律性问题;得到不变的量及变化的量与n的关系是解决本题的关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 若用a表示
若用a表示| 3 | -10 |
| A、A | B、B | C、C | D、D |
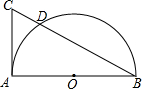 如图所示,AB为⊙O的直径,CA⊥AB,CD=1cm,DB=5cm,则AB=
如图所示,AB为⊙O的直径,CA⊥AB,CD=1cm,DB=5cm,则AB=
 如图,△ABC是等腰直角三角形,C是直角顶点.
如图,△ABC是等腰直角三角形,C是直角顶点.