题目内容
3.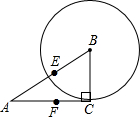 如图.在直角三角形ABC中,∠C=90°,AC=4,BC=3,E,F分别为AB,AC的中点,以B为圆心,BC为半径画圆.试判断点A,C,E,F与⊙B的位置关系.并说明理由.
如图.在直角三角形ABC中,∠C=90°,AC=4,BC=3,E,F分别为AB,AC的中点,以B为圆心,BC为半径画圆.试判断点A,C,E,F与⊙B的位置关系.并说明理由.
分析 求得A、E、F到圆心的距离,与圆的半径进行比较即可作出判断.
解答 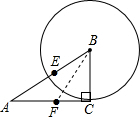 解:连接BF.
解:连接BF.
C在⊙B上;
在直角△ABC中,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5>BC,
则A在⊙B的外部;
BE=$\frac{1}{2}$AB=$\frac{1}{2}$×5=$\frac{5}{2}$<3=BC,则E在⊙B内部;
CF=$\frac{1}{2}$AC=$\frac{1}{2}$×4=2,则在直角△BCF中,BF=$\sqrt{C{F}^{2}+B{C}^{2}}$=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$>BC,则F在⊙B的外部.
点评 本题考查了点和圆的位置关系,关键要记住若半径为r,点到圆心的距离为d,则有:当d>r时,点在圆外;当d=r时,点在圆上,当d<r时,点在圆内.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知线段a,c(a<c),画一个Rt△ABC,使∠C=90°,一直角边CB=a,斜边AB=c.
如图,已知线段a,c(a<c),画一个Rt△ABC,使∠C=90°,一直角边CB=a,斜边AB=c.
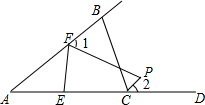 如图,△ABC中,点D在AC的延长线上,E、F分别在边AC和AB上,∠BFE和∠BCD的平分线相交于点P,若∠B=80°,∠FEC=70°,则∠1-∠2=15°°;∠P=95°°.
如图,△ABC中,点D在AC的延长线上,E、F分别在边AC和AB上,∠BFE和∠BCD的平分线相交于点P,若∠B=80°,∠FEC=70°,则∠1-∠2=15°°;∠P=95°°. 如图,平面直角坐标系中,直线AB与x轴,y轴分别交于A(3,0),B(0,$\sqrt{3}$)两点,点C、D分别为线段AB、OA上的一动点.
如图,平面直角坐标系中,直线AB与x轴,y轴分别交于A(3,0),B(0,$\sqrt{3}$)两点,点C、D分别为线段AB、OA上的一动点.