题目内容
9.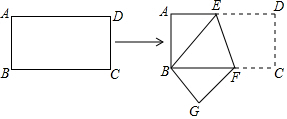 如图所示,长方形纸片ABCD的长AD=8cm,宽AB=4cm,将其折叠,使点D与点B重合.
如图所示,长方形纸片ABCD的长AD=8cm,宽AB=4cm,将其折叠,使点D与点B重合.(1)求证:BE=BF;
(2)求折叠后DE的长;
(2)求以折痕EF为边的正方形面积.
分析 (1)先根据平行线的性质得出∠DEF=∠EFB,再由图形翻折变换的性质得出∠DEF=∠BEF,故可得出∠EFB=∠BEF,进而得出结论;
(2)设DE=xcm,则BE=xcm,AE=(8-x)cm,在Rt△ABE中,利用勾股定理求出x的值即可;
(3)过E作EH⊥BF于点H,则EH=AB=4,BH=AE=3,利用勾股定理求出EF的长即可.
解答 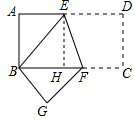 解:(1)在长方形ABCD中,AD∥BC
解:(1)在长方形ABCD中,AD∥BC
∴∠DEF=∠EFB.
∵∠DEF=∠BEF,
∴∠EFB=∠BEF,
∴BE=BF;
(2)设DE=xcm,则BE=xcm,AE=(8-x)cm,
在Rt△ABE中,由勾股定理42+(8-x) 2=x2,
∴x=5,即DE的长为5cm.
(3)过E作EH⊥BF于点H,
∵EH=AB=4,BH=AE=3
∴HF=BF-BH=5-3=2,
∴EF2=22+42=20,
∴以EF为边长的正方形的面积为20cm2.
点评 本题考查的是翻折变换,熟知图形翻折不变性的性质是解答此题的关键.

练习册系列答案
相关题目
19.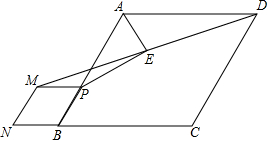 如图,在菱形ABCD中,tan∠ABC=$\frac{4}{3}$,P为AB上一点,以PB为边向外作菱形PMNB,连结DM,取DM中点E,连结AE,PE,则$\frac{AE}{PE}$的值为( )
如图,在菱形ABCD中,tan∠ABC=$\frac{4}{3}$,P为AB上一点,以PB为边向外作菱形PMNB,连结DM,取DM中点E,连结AE,PE,则$\frac{AE}{PE}$的值为( )
 如图,在菱形ABCD中,tan∠ABC=$\frac{4}{3}$,P为AB上一点,以PB为边向外作菱形PMNB,连结DM,取DM中点E,连结AE,PE,则$\frac{AE}{PE}$的值为( )
如图,在菱形ABCD中,tan∠ABC=$\frac{4}{3}$,P为AB上一点,以PB为边向外作菱形PMNB,连结DM,取DM中点E,连结AE,PE,则$\frac{AE}{PE}$的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
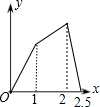
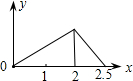
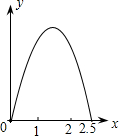
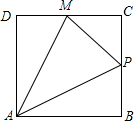 如图,在边长为1的正方形ABCD的边上有一点P按A→B→C→M的顺序运动,M是边CD上的中点,设点P经过的路程x为自变量,△APM的面积为y,则函数的大致图象是( )
如图,在边长为1的正方形ABCD的边上有一点P按A→B→C→M的顺序运动,M是边CD上的中点,设点P经过的路程x为自变量,△APM的面积为y,则函数的大致图象是( )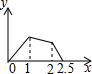
 如图,边长为1的小正方形网格中,⊙O的半径为1,点O及点A、B、C、E都在格点上,则∠AED的正弦值是$\frac{\sqrt{5}}{5}$.
如图,边长为1的小正方形网格中,⊙O的半径为1,点O及点A、B、C、E都在格点上,则∠AED的正弦值是$\frac{\sqrt{5}}{5}$.