题目内容
已知正比例函数y=kx与反比例函数y=| 3 | x |
分析：只需把已知的交点的坐标代入解析式，即可求解；
能够根据对称的性质，求得另一个交点的坐标．
能够根据对称的性质，求得另一个交点的坐标．
解答：解：∵点A（m，1）过反比例函数y=
的图象，
则有1=
，
∴m=3．
又正比例函数y=kx，
∴1=3k，
∴k=
．
另一个交点和点A关于原点对称，
∴坐标为（-3，-1）．
∴正比例函数解析式为y=
x，另一个交点的坐标为（-3，-1）．
故答案为：y=
x；（-3，-1）．
| 3 |
| x |
则有1=
| 3 |
| m |
∴m=3．
又正比例函数y=kx，
∴1=3k，
∴k=
| 1 |
| 3 |
另一个交点和点A关于原点对称，
∴坐标为（-3，-1）．
∴正比例函数解析式为y=
| 1 |
| 3 |
故答案为：y=
| 1 |
| 3 |
点评：本题利用了待定系数法确定m，k的值，并且用到了过原点的直线与反比例函数图象的两个交点坐标关于原点对称的知识．
练习册系列答案
中考利剑中考试卷汇编系列答案
相关题目
已知正比例函数y=k1x（k1≠0）与反比例函数y=
（k2≠0）的图象有一个交点的坐标为（-2，-1），则它的另一个交点的坐标是（ ）
| k2 |
| x |
| A、（2，1） |
| B、（-2，-1） |
| C、（-2，1） |
| D、（2，-1） |
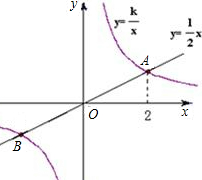横坐标为2．
如图，已知正比例函数和反比例函数的图象都经过点A（3，3）．