题目内容
已知⊙C经过原点O,与x轴正半轴交于A点,与y轴交于B(0,2),P为第一象限内⊙C上一点,且∠APO=30°,求点A及圆心C的坐标.
考点:圆周角定理,坐标与图形性质,解直角三角形
专题:
分析:首先根据题意画出图形,再根据圆周角定理可得∠ABO=30°,∠AOC=60°,根据直角三角形的性质可得AB=4,再根据勾股定理计算出AO,然后利用等腰三角形的性质可得DO和CO,进而得到C点坐标.
解答: 解:过C作CD⊥AO,连接AB、CO,
解:过C作CD⊥AO,连接AB、CO,
由坐标系可知∠BOA=90°,
∵∠APO=30°,
∴∠ABO=30°,∠AOC=60°,
∵B(0,2),
∴BO=2,
∴AB=4,
∴AO=
=2
,
∴A(2
,0);
∵CD⊥AO,
∴DO=
,
CD=
=3,
∴C(
,3).
 解:过C作CD⊥AO,连接AB、CO,
解:过C作CD⊥AO,连接AB、CO,由坐标系可知∠BOA=90°,
∵∠APO=30°,
∴∠ABO=30°,∠AOC=60°,
∵B(0,2),
∴BO=2,
∴AB=4,
∴AO=
| 16-4 |
| 3 |
∴A(2
| 3 |
∵CD⊥AO,
∴DO=
| 3 |
CD=
| 12-3 |
∴C(
| 3 |
点评:本题主要考查了圆周角定理,以及勾股定理的应用和等腰三角形的性质,关键是掌握一条弧所对的圆周角等于它所对的圆心角的一半.

练习册系列答案
相关题目

 已知图中,四边形ABCD为⊙O的内接四边形,E为AB延长线上一点,且∠AOC=80°,则∠D=
已知图中,四边形ABCD为⊙O的内接四边形,E为AB延长线上一点,且∠AOC=80°,则∠D=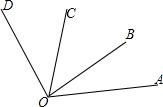 如图所示,∠AOB=35°,∠AOD=105°,∠COA=70°,试问在图中,哪条射线是哪个角的角平分线?
如图所示,∠AOB=35°,∠AOD=105°,∠COA=70°,试问在图中,哪条射线是哪个角的角平分线?