题目内容
15.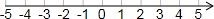 解不等式组:$\left\{\begin{array}{l}{\frac{x+2}{3}<1}\\{2(1-x)≤5}\end{array}\right.$把解集在数轴上表示出来,并将解集中的整数解写出来.
解不等式组:$\left\{\begin{array}{l}{\frac{x+2}{3}<1}\\{2(1-x)≤5}\end{array}\right.$把解集在数轴上表示出来,并将解集中的整数解写出来.
分析 分别计算出两个不等式的解集,再根据大小小大中间找确定不等式组的解集即可,再找出解集范围内的整数即可.
解答 解:$\left\{\begin{array}{l}{\frac{x+2}{3}<1①}\\{2(1-x)≤5②}\end{array}\right.$
由①得:x<1;
由②得:x≥-$\frac{3}{2}$;
∴不等式组的解集为-$\frac{3}{2}$≤x<1.
则不等式组的整数解为-1,0.
点评 此题主要考查了解一元一次不等式组,解决此类问题的关键在于正确解得不等式组或不等式的解集,然后再根据题目中对于解集的限制得到下一步所需要的条件,再根据得到的条件进而求得不等式组的整数解.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
5.某超市货架上摆放着外观、颜色、样式、规格完全相同的盒装酸奶,其生产日期有三盒是“20150410”,五盒是“20150412”,两盒是“20150413”.若从中随机抽取一盒,恰好抽到生产日期为“20150413”的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
20.在等腰△ABC中,AB=AC,其周长为16cm,则AB边的取值范围是( )
| A. | 1cm<AB<4cm | B. | 3cm<AB<6cm | C. | 4cm<AB<8cm | D. | 5cm<AB<10cm |

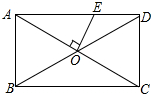 如图,矩形ABCD的对角线AC、BD相交于点O,过点O作OE⊥AC交AD于E,若AB=6,AD=8,求sin∠OEA的值.
如图,矩形ABCD的对角线AC、BD相交于点O,过点O作OE⊥AC交AD于E,若AB=6,AD=8,求sin∠OEA的值. 如图,∠B=70°,∠ACE=140°,CD平分∠ACE,请说明:AB∥CD.
如图,∠B=70°,∠ACE=140°,CD平分∠ACE,请说明:AB∥CD.