题目内容
9. 如图,∠B=70°,∠ACE=140°,CD平分∠ACE,请说明:AB∥CD.
如图,∠B=70°,∠ACE=140°,CD平分∠ACE,请说明:AB∥CD.
分析 先由CD平分∠ACE,根据角平分线定义得出∠DCE=$\frac{1}{2}$∠ACE=70°,那么∠B=∠DCE,再根据同位角相等,两直线平行即可说明AB∥CD.
解答 证明:∵CD平分∠ACE,∠ACE=140°,
∴∠DCE=$\frac{1}{2}$∠ACE=70°,
∵∠B=70°,
∴∠B=∠DCE,
∴AB∥CD.
点评 本题考查了平行线的判定:同位角相等,两直线平行.内错角相等,两直线平行.同旁内角互补,两直线平行.也考查了角平分线定义.

练习册系列答案
相关题目
14.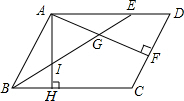 在?ABCD中,BE平分∠ABC交AD于点E,AF⊥CD于点F,交BE于点G,AH⊥BC于点H,交BE于点I.若BI=IG,且AI=3,则AE的长为( )
在?ABCD中,BE平分∠ABC交AD于点E,AF⊥CD于点F,交BE于点G,AH⊥BC于点H,交BE于点I.若BI=IG,且AI=3,则AE的长为( )
 在?ABCD中,BE平分∠ABC交AD于点E,AF⊥CD于点F,交BE于点G,AH⊥BC于点H,交BE于点I.若BI=IG,且AI=3,则AE的长为( )
在?ABCD中,BE平分∠ABC交AD于点E,AF⊥CD于点F,交BE于点G,AH⊥BC于点H,交BE于点I.若BI=IG,且AI=3,则AE的长为( )| A. | 3 | B. | 2$\sqrt{3}$ | C. | 6 | D. | 3$\sqrt{3}$ |
1.下列运算中正确的是( )
| A. | (x3)2=x5 | B. | x5•x2=x10 | C. | x3+x2=x5 | D. | 6x6÷3x2=2x4 |
18.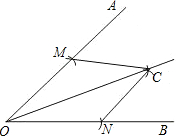 如图,已知∠AOB,按照以下步骤画图:
如图,已知∠AOB,按照以下步骤画图:
(1)以O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以点M、N为圆心,大于$\frac{1}{2}$MN的长半径画弧,两弧在∠AOB内部相交于点C.
(3)作射线OC.
则判断△OMC≌△ONC的依据是( )
 如图,已知∠AOB,按照以下步骤画图:
如图,已知∠AOB,按照以下步骤画图:(1)以O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以点M、N为圆心,大于$\frac{1}{2}$MN的长半径画弧,两弧在∠AOB内部相交于点C.
(3)作射线OC.
则判断△OMC≌△ONC的依据是( )
| A. | 边边边 | B. | 边角边 | C. | 角边角 | D. | 角角边 |
19.已知等腰三角形的两条边长分别为2和3,则它的周长为( )
| A. | 7 | B. | 8 | C. | 5 | D. | 7或8 |
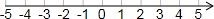 解不等式组:$\left\{\begin{array}{l}{\frac{x+2}{3}<1}\\{2(1-x)≤5}\end{array}\right.$把解集在数轴上表示出来,并将解集中的整数解写出来.
解不等式组:$\left\{\begin{array}{l}{\frac{x+2}{3}<1}\\{2(1-x)≤5}\end{array}\right.$把解集在数轴上表示出来,并将解集中的整数解写出来. 某公园管理人员在巡视公园时,发现有一条圆柱形的输水管道破裂,通知维修人员到场检测,维修员画出水平放置的破裂管道有水部分的截面图(如图).
某公园管理人员在巡视公园时,发现有一条圆柱形的输水管道破裂,通知维修人员到场检测,维修员画出水平放置的破裂管道有水部分的截面图(如图).