题目内容
已知:a2-b2=(a-b)(a+b);a3-b3=(a-b)(a2+ab+b2);a4-b4=(a-b)(a3+a2b+ab2+b3);按此规律,则:
(1)a5-b5=(a-b) ;
(2)若a-
=2,根据上述规律求出代数式a3-(
)3的值等于 .
(1)a5-b5=(a-b)
(2)若a-
| 1 |
| a |
| 1 |
| a |
考点:因式分解的应用
专题:规律型
分析:(1)根据题意,按同一个字母的降幂排列直至不含这个字母为止;
(2)根据规律,先把代数式a3--(
)3分解因式,再代入计算即可.
(2)根据规律,先把代数式a3--(
| 1 |
| a |
解答:解:(1)a5-b5=(a-b)(a4+a3b+a2b2+ab3+b4);
(2)a3-(
)3=(a-
)(a2+1+
)
=(a-
)(a2-2+
+3)
=(a-
)[(a-
)2+3]
=2×(4+3)
=2×7
=14.
故答案为:a4+a3b+a2b2+ab3+b4;14.
(2)a3-(
| 1 |
| a |
| 1 |
| a |
| 1 |
| a2 |
=(a-
| 1 |
| a |
| 1 |
| a3 |
=(a-
| 1 |
| a |
| 1 |
| a |
=2×(4+3)
=2×7
=14.
故答案为:a4+a3b+a2b2+ab3+b4;14.
点评:此题考查因式分解的灵活运用,正确利用类比的方法得出答案解决问题.

练习册系列答案
相关题目
已知x-y=2,x-z=
,则(y-z)2-2(y-z)+
的值为( )
| 1 |
| 2 |
| 3 |
| 4 |
| A、6 | ||
B、
| ||
| C、3 | ||
| D、0 |
 如图,在矩形AOBC中,点A的坐标是(-3,1),点C的纵坐标是7,则B、C两点的坐标分别是( )
如图,在矩形AOBC中,点A的坐标是(-3,1),点C的纵坐标是7,则B、C两点的坐标分别是( )| A、(2,6)、(-1,7) | ||||||
B、(2,6)、(-
| ||||||
C、(
| ||||||
D、(
|
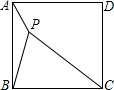 已知如图,正方形ABCD中,P是内部一点,且点P到A、B、C三点的距离分别是1、2、3,则图中∠APB的度数是( )
已知如图,正方形ABCD中,P是内部一点,且点P到A、B、C三点的距离分别是1、2、3,则图中∠APB的度数是( )| A、120? | B、125? |
| C、135? | D、150? |

 如图:三角形有
如图:三角形有