题目内容
3．
如图，在平面直角坐标系中，抛物线y=ax2+3与y轴交于点A，过点A与x轴平行的直线交抛物线y=$\frac{1}{3}$x2于B、C两点，则BC的长为（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 6 |
分析 先由y轴上点的横坐标为0求出A点坐标为（0，3），再将y=3代入y=$\frac{1}{3}$x2，求出x的值，得出B、C两点的坐标，进而求出BC的长度．
解答 解：∵抛物线y=ax2+3与y轴交于点A，
∴A点坐标为（0，3）．
当y=3时，$\frac{1}{3}$x2=3，
解得x=±3，
∴B点坐标为（-3，3），C点坐标为（3，3），
∴BC=3-（-3）=6．
故选D．
点评 本题考查了二次函数图象上点的坐标特征，两函数交点坐标的求法，平行于x轴上的两点之间的距离，比较简单．
练习册系列答案
相关题目
如图，在平面直角坐标系中，点A（2，n），B（m，n）（m＞2），D（p，q）（q＜n），点B，D在直线y=$\frac{1}{2}$x+1上．四边形ABCD的对角线AC，BD相交于点E，且AB∥CD，CD=4，BE=DE，△AEB的面积是2．
6．
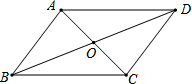如图，?ABCD的对角线AC、BD相交于点O，则下列说法一定正确的是（ ）
如图，?ABCD的对角线AC、BD相交于点O，则下列说法一定正确的是（ ）| A． | AO=OD | B． | AO⊥OD | C． | AO=OC | D． | AO⊥AB |
8．下列各数中，最小的数是（ ）
| A． | -0.5 | B． | 0 | C． | -2 | D． | 1 |
12．-$\frac{1}{2015}$的倒数为（ ）
| A． | -2015 | B． | -$\frac{1}{2015}$ | C． | 2015 | D． | $\frac{1}{2015}$ |