题目内容
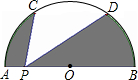 如图,AB是半⊙O的直径,C、D是半圆的三等分点,若AB=2,P是直径AB上的任意一点,则图中阴影部分的面积是________.
如图,AB是半⊙O的直径,C、D是半圆的三等分点,若AB=2,P是直径AB上的任意一点,则图中阴影部分的面积是________.

分析:连CD,OC,OD,根据圆周角定理得到∠AOC=∠COD=∠BOD,则∠AOC=∠COD=60°,得到△OCD为等边三角形,则∠OCD=60°,判断CD∥AB,得到S△PCD=S△OCD,则阴影部分的面积=S半圆-S扇形OCD,然后利用圆的面积公式和扇形的面积公式计算即可.
解答:
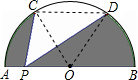 解:连CD,OC,OD,如图,
解:连CD,OC,OD,如图,∵AB是半⊙O的直径,C、D是半圆的三等分点,
∴∠AOC=∠COD=∠BOD,
∴∠AOC=∠COD=60°,
∴△OCD为等边三角形,
∴∠OCD=60°,
∴CD∥AB,
∴S△PCD=S△OCD,
∴阴影部分的面积=S半圆-S扇形OCD,
=
 π•12-
π•12-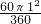 ,
,=
 π.
π.故答案为:
 π.
π.点评:本题考查了扇形的面积公式:S=
 .也考查了圆周角定理、等边三角形的性质以及三角形的面积公式.
.也考查了圆周角定理、等边三角形的性质以及三角形的面积公式. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
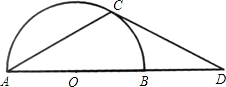 如图,AB是半⊙O的直径,弦AC与AB成30°的角,AC=CD.
如图,AB是半⊙O的直径,弦AC与AB成30°的角,AC=CD.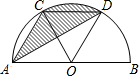 如图,AB是半⊙O的直径,C、D是半圆的三等分点,半圆的半径为R.
如图,AB是半⊙O的直径,C、D是半圆的三等分点,半圆的半径为R.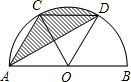 如图,AB是半⊙O的直径,C、D是半圆的三等分点,半圆的半径为4.阴影部分的面积为
如图,AB是半⊙O的直径,C、D是半圆的三等分点,半圆的半径为4.阴影部分的面积为 (2012•密云县二模)如图,AB是半⊙O的直径,C是⊙O上一点,OD⊥BC于D,若AC:BC=4:3,AB=10cm,则OD的长为( )
(2012•密云县二模)如图,AB是半⊙O的直径,C是⊙O上一点,OD⊥BC于D,若AC:BC=4:3,AB=10cm,则OD的长为( ) 如图,AB是半⊙O的直径,点C是半⊙O的三等分点,设扇形AOC、△COB、弓形BPC的面积分别为S1、S2、S3,则它们的大小关系为
如图,AB是半⊙O的直径,点C是半⊙O的三等分点,设扇形AOC、△COB、弓形BPC的面积分别为S1、S2、S3,则它们的大小关系为