题目内容
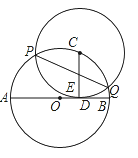
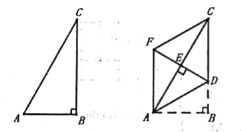
【题目】⊙O的半径为5，AB是⊙O的直径，点C在⊙O上，点D在直线AB上.
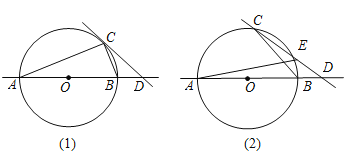
（1）如图（1），已知∠BCD=∠BAC，求证：CD是⊙O的切线；
（2）如图（2），CD与⊙O交于另一点E，BD：DE：EC=2；3：5求圆心O到直线CD的距离；
（3）若图（2）中的点D是直线AB上的动点，点D在运动过程中，会出现在C，D，E三点中，其中一点是另两点连线的中点的情况，问这样的情况出现几次？
【答案】（1）证明见解析；（2）
；（3）三次.
【解析】
试题（1）连接OC，证明OC⊥CD即可.
（2）连接OC、OE，过点O作OF⊥CE于点F，证明△BCD∽△EAD，得比例式
，即
，根据BD：DE：EC=2：3：5，可设BD=2k，DE=3k，EC=5k，代入求出k即可得BD=2，DE=3，EC=5，从而根据勾股定理即可求得OF.
（3）分点D在⊙O外，点E是CD中点和点D在⊙O内，点D是CE中点两种情况讨论即可.
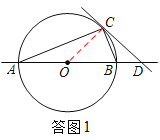
试题解析：解：（1）证明：如答图1，连接OC，
∵OA=OC，∴∠OAC=∠OCA.
又∵AB是⊙O的直径，∴∠ACB=90°.
又∵∠BCD=∠BAC，∴∠BCD =∠OCA.
∴∠OCD=∠BCD +∠OCB=90°，即OC⊥CD.
∴CD是⊙O的切线.
（2）如答图2，∵∠ADE=∠CDB，∠BCD=∠EAD，∴△BCD∽△EAD.
∴，即.
又∵BD：DE：EC=2：3：5，∴可设BD=2k，DE=3k，EC=5k.
又∵⊙O的半径为5，∴
，解得k=1.
∴BD=2，DE=3，EC=5.
连接OC、OE，过点O作OF⊥CE于点F，
则△OEC是等边三角形， EF=
CE=
.
∴根据勾股定理得
OF=
.
∴圆心O到直线CD的距离是.
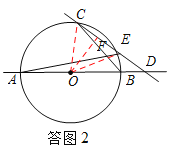
（3）这样的情形共有出现三次：当点D在⊙O外时，点E是CD中点，有如答图3，4的两种情形；当点D在⊙O内时，点D是CE中点，有如答图5的一种情形.
