Question

【题目】阅读资料，解决问题．

人教版《数学九年级（下册）》的页有这样一个思考问题：

问题：如图，在中，交，于点，，如果通过“相似的定义”证明？

根据“两直线平行，同位角相等”容易得出三对对应角分别相等，再根据“平行线分线段成比例”的基本事实，容易得出，所以这个问题的核心时如何证明“”．

证明思路：过点作交于点，构造平行四边形，得到，从而将比例式中的，转化为共线的两条线段，，同时也构造了基本图形“”，得到，从而得证．

解决问题：

（）①类比资料中的证明思路，请你证明“三角形内角平分线定理”．

三角形内角平分线定理：三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例．

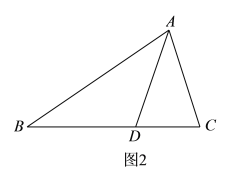
已知：如图，中，是角平分线．

求证：．

②运用“三角形内角平分线定理”填空：

已知：如图，中，是角平分线，，，，则__________．

（）我们知道，如果两个三角形有相同的高或者相等的高，那么它们面积的比就等于底的比．

请你通过研究和面积的比来证明三角形内角平分线定理．

已知：如图，中，是角平分线．

求证：．

Answer 1

【答案】（）①证明见解析② （2）证明见解析

【解析】

（1）①如图过点作的平行线交的延长线于点，然后说明，利用相似三角形的性质即可完成证明;②设,然后利用（1）的结论和已知条件即可完成解答; （）过点作，的垂线，垂足为、，

过点作的垂线，垂足为;先利用角平分线定理说明，然后再利用等面积法得到和，从而得到，即.

（）①证明：过点作的平行线交的延长线于点，

∴，

又∵平分，

∵，

∴，

∴，

又∵，

∴，

∴，

∴．

②设，

∴，

又∵，

∴，

∴，

∴，

．

（）过点作，的垂线，垂足为、，

过点作的垂线，垂足为，

∵为的角分线，

∴，

，

又∵，

∴，

∴．