��Ŀ����
��ͼ��1��������y=ax2+bx+c��a��o���Ķ���ΪC��1��4������x����A��B���㣬��y���ڵ�D�����е�B������Ϊ��3��0��
��1���������ߵĺ�������ʽ��
��2����ͼ��2��T���������ϵ�һ�㣬����T��x��Ĵ��ߣ�����Ϊ��M������M��MN��BD�����߶�AD�ڵ�N������MD������DNM�ס�BMD�����T�����ꣻ
��3����ͼ��3��������A��ֱ�����������ཻ��E����E��ĺ�����Ϊ2����y�ύ�ڵ�F��ֱ��PQ�������ߵĶԳ��ᣬG��ֱ��PQ�ϵ�һ���㣬��̽����x�����Ƿ����һ��H��ʹD��G��H��F�ĵ�Χ�ɵ��ı����ܳ���С�������ڣ���������Сֵ����G��H�����ꣻ�������ڣ���˵�����ɣ�

��1���������ߵĺ�������ʽ��
��2����ͼ��2��T���������ϵ�һ�㣬����T��x��Ĵ��ߣ�����Ϊ��M������M��MN��BD�����߶�AD�ڵ�N������MD������DNM�ס�BMD�����T�����ꣻ
��3����ͼ��3��������A��ֱ�����������ཻ��E����E��ĺ�����Ϊ2����y�ύ�ڵ�F��ֱ��PQ�������ߵĶԳ��ᣬG��ֱ��PQ�ϵ�һ���㣬��̽����x�����Ƿ����һ��H��ʹD��G��H��F�ĵ�Χ�ɵ��ı����ܳ���С�������ڣ���������Сֵ����G��H�����ꣻ�������ڣ���˵�����ɣ�

��������1���������ߵĽ���ʽΪ��y=a��x-1��2+4��Ȼ��B��������뺯������ʽ������ô������ߵĽ���ʽ��
��2��������M������Ϊ��m��0�������BD��DM�ij�����ƽ���߷��߶γɱ������������MN�ij���Ȼ�������������ζ�Ӧ�߳ɱ��������ɵ�DM2=BD•MN����ɵõ�����m��һԪ���η��̣��ⷽ�̼�����ô𰸣�
��3����F����x��ĶԳƵ�F�䣨0��-1��������EF�佻x����H�����Գ���x=1��G���ı���DFHG���ܳ���Ϊ��С����������⼴����������Сֵ����G��H�����꣮
��2��������M������Ϊ��m��0�������BD��DM�ij�����ƽ���߷��߶γɱ������������MN�ij���Ȼ�������������ζ�Ӧ�߳ɱ��������ɵ�DM2=BD•MN����ɵõ�����m��һԪ���η��̣��ⷽ�̼�����ô𰸣�
��3����F����x��ĶԳƵ�F�䣨0��-1��������EF�佻x����H�����Գ���x=1��G���ı���DFHG���ܳ���Ϊ��С����������⼴����������Сֵ����G��H�����꣮
����⣺��1���������ߵĽ���ʽΪ��y=a��x-1��2+4��
�ߵ�B������Ϊ��3��0����
��4a+4=0��
��a=-1��
��������ߵĽ���ʽΪ��y=-��x-1��2+4����y=-x2+2x+3��
 ��2����y=-x2+2x+3���൱x=0ʱ��y=3��
��2����y=-x2+2x+3���൱x=0ʱ��y=3��
���D��������0��3����
�ߵ�B������Ϊ��3��0����
��BD=
=3
��
��M��m��0������DM=
��
��MN��BD��
��
=
����
=
��
��MN=
��1+m����
�ߡ�DNM�ס�BMD��
��
=
����DM2=BD•MN��
��9+m2=3
��
��1+m����
��ã�m=
��m=3����ȥ����
��m=
ʱ��y=-��
-1��2+4=
��
�������T��������
��
����
 ��3����x���ϴ���һ��H���ܹ�ʹD��G��H��F�ĵ�Χ�ɵ��ı����ܳ���С���������£�
��3����x���ϴ���һ��H���ܹ�ʹD��G��H��F�ĵ�Χ�ɵ��ı����ܳ���С���������£�
��y=-x2+2x+3���Գ��᷽��Ϊ��x=1��
�൱x=2ʱ��y=-4+4+3=3��
���E��2��3����
����ֱ��AE�Ľ���ʽΪ��y=kx+n��
��
�����
��
��ֱ��AE�Ľ���ʽΪ��y=x+1��
���F��0��1����
��D��0��3����
��D��E����x=1�Գƣ�
����F����x��ĶԳƵ�F�䣨0��-1��������EF�佻x����H�����Գ���x=1��G�����ı���DFHG���ܳ���Ϊ��С��
��ֱ��EF��Ľ���ʽΪ��y=px+q��
��
����ã�
��
��ֱ��EF��Ľ���ʽΪ��y=2x-1��
�൱y=0ʱ��2x-1=0����x=
����H��
��0����
��x=1ʱ��y=1����G��1��1����
��DF=2��FH=F��H=
=
��DG=
=
��
��ʹD��G��H��F�ĵ���Χ�ɵ��ı����ܳ���СֵΪ��DF+FH+GH+DG=2+
+
+
=2+2
��
�ߵ�B������Ϊ��3��0����
��4a+4=0��
��a=-1��
��������ߵĽ���ʽΪ��y=-��x-1��2+4����y=-x2+2x+3��
 ��2����y=-x2+2x+3���൱x=0ʱ��y=3��
��2����y=-x2+2x+3���൱x=0ʱ��y=3�����D������Ϊ��0��3����
�ߵ�B������Ϊ��3��0����
��BD=
| 32+32 |
| 2 |
��M��m��0������DM=
| 32+m2 |
��MN��BD��
��
| MN |
| BD |
| AM |
| AB |
| MN | ||
3
|
| 1+m |
| 4 |
��MN=
3
| ||
| 4 |
�ߡ�DNM�ס�BMD��
��
| DM |
| BD |
| MN |
| DM |
��9+m2=3
| 2 |
3
| ||
| 4 |
��ã�m=
| 3 |
| 2 |
��m=
| 3 |
| 2 |
| 3 |
| 2 |
| 15 |
| 4 |
�������T��������
| 3 |
| 2 |
| 15 |
| 4 |
 ��3����x���ϴ���һ��H���ܹ�ʹD��G��H��F�ĵ�Χ�ɵ��ı����ܳ���С���������£�
��3����x���ϴ���һ��H���ܹ�ʹD��G��H��F�ĵ�Χ�ɵ��ı����ܳ���С���������£���y=-x2+2x+3���Գ��᷽��Ϊ��x=1��
�൱x=2ʱ��y=-4+4+3=3��
���E��2��3����
����ֱ��AE�Ľ���ʽΪ��y=kx+n��
��
|
|
��ֱ��AE�Ľ���ʽΪ��y=x+1��
���F��0��1����
��D��0��3����
��D��E����x=1�Գƣ�
����F����x��ĶԳƵ�F�䣨0��-1��������EF�佻x����H�����Գ���x=1��G�����ı���DFHG���ܳ���Ϊ��С��
��ֱ��EF��Ľ���ʽΪ��y=px+q��
��
|
|
��ֱ��EF��Ľ���ʽΪ��y=2x-1��
�൱y=0ʱ��2x-1=0����x=
| 1 |
| 2 |
| 1 |
| 2 |
��x=1ʱ��y=1����G��1��1����
��DF=2��FH=F��H=
12+(
|
| ||
| 2 |
| 12+22 |
| 5 |
��ʹD��G��H��F�ĵ���Χ�ɵ��ı����ܳ���СֵΪ��DF+FH+GH+DG=2+
| ||
| 2 |
| ||
| 2 |
| 5 |
| 5 |
���������⿼���˶��κ������ۺ����ͣ������漰����֪ʶ�������ô���ϵ������һ�κ��������κ��������Ľ���ʽ��ƽ���߷��߶γɱ�����������Գ�-���·�����⣬���������ε��ж������ʵ�֪ʶ�������ۺ��Ժ�ǿ������Ĺؼ���ע�����ν��˼���Ӧ�ã�

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
 ��m��0��
��m��0�� ��C��OA=OB��BC��x�ᣮ
��C��OA=OB��BC��x�ᣮ ��ͼ��һ��������y=ax2+bx��a��0���Ķ�������Ϊ��2��
��ͼ��һ��������y=ax2+bx��a��0���Ķ�������Ϊ��2��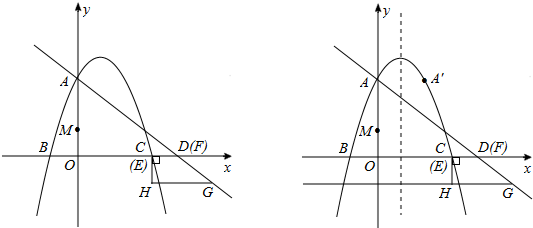
 ��ͼ����֪������y=-x2+2x+3��x����A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��
��ͼ����֪������y=-x2+2x+3��x����A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��