题目内容
 反比例函数y=
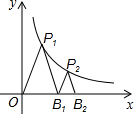
反比例函数y= (m>0)第一象限内的图象如图所示,△OP1B1,△B1P2B2均为等腰三角形,且OP1∥B1P2,其中点P1,P2在反比例函数y=
(m>0)第一象限内的图象如图所示,△OP1B1,△B1P2B2均为等腰三角形,且OP1∥B1P2,其中点P1,P2在反比例函数y= (m>0)的图象上,点B1,B2在x轴上,则
(m>0)的图象上,点B1,B2在x轴上,则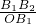 的值为________.
的值为________.
 -1
-1分析:作P1A⊥x轴于A,P2C⊥x轴于C,可设P1点的坐标为(a,
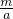 ),P2点的坐标为(b,
),P2点的坐标为(b, ),根据等腰三角形的性质得OA=B1A,B1C=CB2,则OA=a,OB1=2a,B1C=b-2a,B1B2=2(b-2a),由于OP1∥B1P2,根据三角形相似的判定易得Rt△P1OA∽Rt△P2B1C,则OA:B1C=P1A:P2C,即a:(b-2a)=
),根据等腰三角形的性质得OA=B1A,B1C=CB2,则OA=a,OB1=2a,B1C=b-2a,B1B2=2(b-2a),由于OP1∥B1P2,根据三角形相似的判定易得Rt△P1OA∽Rt△P2B1C,则OA:B1C=P1A:P2C,即a:(b-2a)=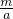 :
: ,可得到a=(
,可得到a=( -1)b或a=(-
-1)b或a=(- -1)b(舍去),于是B1B2=2(b-2a)=(6-4
-1)b(舍去),于是B1B2=2(b-2a)=(6-4 )b,然后进行二次根式运算得到
)b,然后进行二次根式运算得到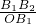 =
=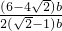 =
= -1.
-1.解答:作P1A⊥x轴于A,P2C⊥x轴于C,如图,
设P1点的坐标为(a,
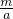 ),P2点的坐标为(b,
),P2点的坐标为(b, ),
),∵△OP1B1,△B1P2B2均为等腰三角形,
∴OA=B1A,B1C=CB2,
∴OA=a,OB1=2a,B1C=b-2a,B1B2=2(b-2a),
∵OP1∥B1P2,
∴∠P1OA=∠CB1P2,
∴Rt△P1OA∽Rt△P2B1C,
∴OA:B1C=P1A:P2C,即a:(b-2a)=
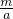 :
: ,
,整理得a2+2ab-b2=0,解得a=(
 -1)b或a=(-
-1)b或a=(- -1)b(舍去),
-1)b(舍去),∴B1B2=2(b-2a)=(6-4
 )b,
)b,∴
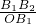 =
=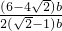 =
= -1.
-1.故答案为
 -1.
-1.点评:本题考查了反比例函数综合题:反比例函数图象上的点满足其解析式;等腰三角形底边上的高是常作的辅助线;运用三角形相似的判定与性质进行几何计算是常见地方法.

练习册系列答案
相关题目
若点(3,4)是反比例函数y=
的图象上一点,则此函数图象必经过点( )
| m2+2m+1 |
| x |
| A、(2,6) |
| B、(-2.6) |
| C、(4,-3) |
| D、(3,-4) |




 如图,点A在反比例函数y=
如图,点A在反比例函数y= 若一次函数y=kx+b的图象如图所示,则抛物线y=x2+kx+b的对称轴位于y轴的
若一次函数y=kx+b的图象如图所示,则抛物线y=x2+kx+b的对称轴位于y轴的