题目内容
8.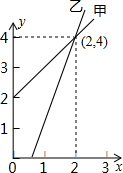 如图,是甲、乙两家商店销售同一种产品的销售价y(元)与销售量x(件)之间的函数图象.下列说法:①售2件时甲、乙两家售价一样;②买1件时买乙家的合算;③买3件时买甲家的合算;④买甲家的1件售价约为3元,其中正确的说法是(填序号)①②③.
如图,是甲、乙两家商店销售同一种产品的销售价y(元)与销售量x(件)之间的函数图象.下列说法:①售2件时甲、乙两家售价一样;②买1件时买乙家的合算;③买3件时买甲家的合算;④买甲家的1件售价约为3元,其中正确的说法是(填序号)①②③.
分析 结合甲、乙的图象位置以及交点(2,4)的意义可以判断①②③结论的成立与否;再由甲图象过(0,2)、(2,4),可知(1,3)在甲的图象上,即买甲家的1件的售价为3元,而不是约为3元,从而得出结论①②③成立.
解答 解:图形中甲乙的交点为(2,4),结合点的意义可知:
售2件时甲、乙两家售价一样,即①成立;
当x=1时,乙的图象在甲的图象的下方,
即买1件时买乙家的合算,②成立;
当x=3时,甲的图象在乙的图象的下方,
即买3件时买甲家的合算,③成立;
甲的图象经过点(0,2)、(2,4),
两点的中点坐标为($\frac{2}{2}$=1,$\frac{2+4}{2}$=3).
即买甲家的1件售价为3元,④不成立.
故答案为:①②③.
点评 本题考查了一次函数的应用、坐标系中点的意义,解题的关键是:结合图象与坐标系中点的意义来判断各说法是否成立.本题属于基础题型,只要理解了坐标系中点的意义结合图形即可解决.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16. 如图,设数轴上的点A,B,C表示的数分别为a,b,c,则下列说法中错误的是( )
如图,设数轴上的点A,B,C表示的数分别为a,b,c,则下列说法中错误的是( )
 如图,设数轴上的点A,B,C表示的数分别为a,b,c,则下列说法中错误的是( )
如图,设数轴上的点A,B,C表示的数分别为a,b,c,则下列说法中错误的是( )| A. | a<0 | B. | b>0 | C. | c>b | D. | a-b>0 |
13.在平面直角坐标系中,若点M的坐标是(m,n),且点M在第二象限,则mn的值( )
| A. | <0 | B. | >0 | C. | =0 | D. | 不能确定 |
20.计算(-$\frac{1}{2}$x3y)2的结果是( )
| A. | $\frac{1}{2}$x4y2 | B. | -$\frac{1}{4}$x6y2 | C. | $\frac{1}{4}$x6y2 | D. | $\frac{1}{2}$x6y2 |
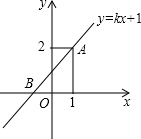 如图,一次函数y=kx+1的图象过点A(1,2),且与x轴相交于点B.若点P是坐标轴上的一点,且满足∠APB=90°,则点P的坐标是P1(1,0),P2(0,1+$\sqrt{2}$),P3(0,1-$\sqrt{2}$).
如图,一次函数y=kx+1的图象过点A(1,2),且与x轴相交于点B.若点P是坐标轴上的一点,且满足∠APB=90°,则点P的坐标是P1(1,0),P2(0,1+$\sqrt{2}$),P3(0,1-$\sqrt{2}$). 浠水县某中学规划在校园内一块长36米,宽20米的矩形场地ABCD上修建三条同样宽的人行道,使其中两条与AB平行,另一条与AD平行,其余部分种草,(如图所示),若使每一块草坪的面积都为96平方米,则人行道的宽为多少米?
浠水县某中学规划在校园内一块长36米,宽20米的矩形场地ABCD上修建三条同样宽的人行道,使其中两条与AB平行,另一条与AD平行,其余部分种草,(如图所示),若使每一块草坪的面积都为96平方米,则人行道的宽为多少米?