题目内容
 如图,在⊙O中,
如图,在⊙O中, 与
与 相等,OD⊥BC,OE⊥AC,垂足分别为D、E,且OD=OE,那么△ABC是什么三角形,为什么?
相等,OD⊥BC,OE⊥AC,垂足分别为D、E,且OD=OE,那么△ABC是什么三角形,为什么?
解:△ABC为等边三角形.理由如下:
连OC,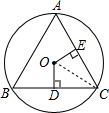
∵ =
= ,
,
∴AB=BC,
∵OD⊥BC,OE⊥AC,
∴CE= AC,CD=
AC,CD= BC,∠ODC=∠OEC=90°
BC,∠ODC=∠OEC=90°
∵在Rt△ODC和Rt△OEC中,
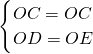 ,
,
∴Rt△ODC≌Rt△OEC(HL)
∴CD=CE,
∴BC=AC,
∴AB=AC=CB,
∴△ABC为等边三角形.
分析:根据圆心角、弧、弦的关系由 =
= 得到AB=BC,再由OD⊥BC,OE⊥AC,根据垂径定理和垂直的定义得到CE=
得到AB=BC,再由OD⊥BC,OE⊥AC,根据垂径定理和垂直的定义得到CE= AC,CD=
AC,CD= BC,∠ODC=∠OEC=90°利用三角形全等的判定方法可得到Rt△ODC≌Rt△OEC(HL),则CD=CE,于是有BC=AC,则AB=AC=CB,即可得到△ABC为等边三角形.
BC,∠ODC=∠OEC=90°利用三角形全等的判定方法可得到Rt△ODC≌Rt△OEC(HL),则CD=CE,于是有BC=AC,则AB=AC=CB,即可得到△ABC为等边三角形.
点评:本题考查了圆心角、弧、弦的关系:在同圆或等圆中两个圆心角、两条弧、两条弦中有一组量相等,那么其余各组量也分别相等.也考查了垂径定理和等边三角形的判定.
连OC,

∵
 =
= ,
,∴AB=BC,
∵OD⊥BC,OE⊥AC,
∴CE=
 AC,CD=
AC,CD= BC,∠ODC=∠OEC=90°
BC,∠ODC=∠OEC=90°∵在Rt△ODC和Rt△OEC中,
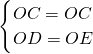 ,
,∴Rt△ODC≌Rt△OEC(HL)
∴CD=CE,
∴BC=AC,
∴AB=AC=CB,
∴△ABC为等边三角形.
分析:根据圆心角、弧、弦的关系由
 =
= 得到AB=BC,再由OD⊥BC,OE⊥AC,根据垂径定理和垂直的定义得到CE=
得到AB=BC,再由OD⊥BC,OE⊥AC,根据垂径定理和垂直的定义得到CE= AC,CD=
AC,CD= BC,∠ODC=∠OEC=90°利用三角形全等的判定方法可得到Rt△ODC≌Rt△OEC(HL),则CD=CE,于是有BC=AC,则AB=AC=CB,即可得到△ABC为等边三角形.
BC,∠ODC=∠OEC=90°利用三角形全等的判定方法可得到Rt△ODC≌Rt△OEC(HL),则CD=CE,于是有BC=AC,则AB=AC=CB,即可得到△ABC为等边三角形.点评:本题考查了圆心角、弧、弦的关系:在同圆或等圆中两个圆心角、两条弧、两条弦中有一组量相等,那么其余各组量也分别相等.也考查了垂径定理和等边三角形的判定.

练习册系列答案
相关题目
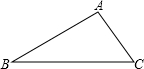 如图,在△ABC中,∠ABC=30°,AB=10,那么以A为圆心,6为半径的⊙A与直线BC的位置关系是( )
如图,在△ABC中,∠ABC=30°,AB=10,那么以A为圆心,6为半径的⊙A与直线BC的位置关系是( )| A、相交 | B、相切 | C、相离 | D、不能确定 |
 如图:在△OAB中放置了3个圆,它们与三角形的边相切,与相邻的圆相外切,已知最大圆与最小圆的半径分别是4、2,那么中间的圆的半径是( )
如图:在△OAB中放置了3个圆,它们与三角形的边相切,与相邻的圆相外切,已知最大圆与最小圆的半径分别是4、2,那么中间的圆的半径是( )| A、3 | ||
B、2
| ||
| C、2.8 | ||
| D、不确定 |
 如图,在△OAB中放置了3个圆,它们与相邻的三角形的边相切,与相邻的圆相外切,已知最大圆与最小圆的半径分别是4、2,那么中间的圆的半径是
如图,在△OAB中放置了3个圆,它们与相邻的三角形的边相切,与相邻的圆相外切,已知最大圆与最小圆的半径分别是4、2,那么中间的圆的半径是 从点B出发沿BC方向以每秒1个单位的速度向点C运动,设运动时间为t秒.
从点B出发沿BC方向以每秒1个单位的速度向点C运动,设运动时间为t秒. 点A和B不重合),以OA为半径的⊙O与AB相交于点E.
点A和B不重合),以OA为半径的⊙O与AB相交于点E.