题目内容

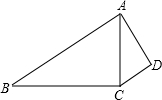
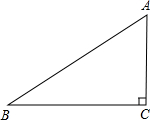
如图，∠ACB=∠ADC=90°，AC=
6
，AD=2．问当AB的长为多少时，这两个直角三角形相似．
∵AC=
6
，AD=2，
∴CD=
AC2-AD2
=
2
．要使这两个直角三角形相似，有两种情况：
（1）当Rt△ABC∽Rt△ACD时，有
AC
AD
=
AB
AC
，∴AB=
AC2
AD
=3；
（2）当Rt△ACB∽Rt△CDA时，有
AC
CD
=
AB
AC
，∴AB=
AC2
CD
=3
2
．
故当AB的长为3或3
2
时，这两个直角三角形相似．
练习册系列答案
相关题目
如图，E、F分别为矩形ABCD的边AD、CD上的点，∠BEF=90°，则图中Ⅰ、Ⅱ、Ⅲ、Ⅳ四个三角形中一定相似的是（　　）
A．Ⅰ和ⅡB．Ⅰ和ⅢC．Ⅱ和ⅢD．Ⅲ和Ⅳ
如图，已知∠ACB=∠CBD=90°，BC=a，AC=b，当CD=（　　）时，△CDB∽△ABC．
A．
a2
b
B．
b2
a
C．
b
a
a2+b2
D．
a
b
a2+b2
已知：△ABC中，∠A=36°，AB=AC，BD平分∠ABC交AC于点O，试说明：△BDC∽△ABC．
如图，AC⊥OB于点C，BD⊥OA于点D，则图中相似三角形共有（　　）
A．3对B．4对C．5对D．6对
如图，AB∥CD，AE∥FD，则图中的相似三角形共有（　　）
A．2对B．4对C．6对D．8对
已知，如图，Rt△ABC中，∠ACB=90°，AB=5，两直角边AC、BC的长是关于x的方程x2-（m+5）x+6m=0的两个实数根．
（1）求m的值及AC、BC的长（BC＞AC）；
（2）在线段BC的延长线上是否存在点D，使得以D、A、C为顶点的三角形与△ABC相似？若存在，求出CD的长；若不存在，请说明理由．
如图，四边形ABCD的对角线AC与BD相交于点O，∠ADO=∠BCO
求证：△ABO∽△DCO．
如图，AB是斜靠在墙上的梯子，梯脚B距墙2m，梯上的点D距墙1.2m，BD的长为1.2m，其中△ADE∽△ABC，梯子AB的长为______m．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网